Hai lực thành phần có độ lớn là F1=F2=b. F1 hợp với F2 một góc 90 độ. Biết rằng độ lớn hợp lực của hai lực trên là F = 14\(\sqrt{2}\). Xác định b.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


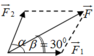
Vì F 1 = F 2 mà F 1 → ; F 2 → tạo thành hình bình hành với đường chéo là F → nên α = 2 β = 2.30 0 = 60 0
Ta có F = 2. F 1 cos α 2
⇒ F = 2.50. 3 . cos 30 0 = 100. 3 . 3 2 = 150 N

Chọn đáp án C
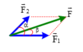
Quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng:
![]()
Với:
F2 = F12 + F22 + 2F1F2cosa
![]()

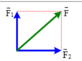
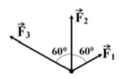


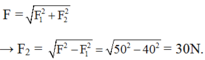
Ta có: \(\overrightarrow{F_{hl}}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
Lại có: \(\alpha=\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)\)
\(F_1\)hợp với \(F_2\) một góc là \(90^o\).
\(F_{hl}=\sqrt{F_1^2+F_2^2+2F_1F_2cos\alpha}\) \(=\sqrt{b^2+b^2+2\cdot b\cdot b\cdot cos90^o}\) \(=\sqrt{2b^2+2b^2\cdot0}=\sqrt{2b^2}\)Mà \(F_{hl}=14\sqrt{2}N\)\(\Rightarrow\sqrt{2b^2}=14\sqrt{2}\)Bình phương hai vế ta đc: \(2b^2=\left(14\sqrt{2}\right)^2=392\)
\(\Rightarrow b^2=196\Rightarrow b=14N\)