Tìm tọa độ giao điểm M của đồ thị hàm số y = x - 1 x + 2 với trục tung
A. ( 0 ; 1 2 )
B. ( 0 ; - 1 2 )
C. ( 0 ; 1 3 )
D. ( 0 ; - 1 3 )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

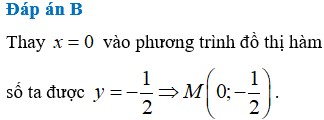

a) Đồ thị:

b) Gọi giao điểm của đồ thị của hàm số y = x - 1 với trục tung, với trục hoành lần lượt là 2 điểm B và C
Thay x = 0 vào hàm số y = x - 1 ta có:
y = 0 - 1 = - 1
⇒ B(0; -1)
Thay y = 0 vào hàm số y = x - 1 ta có:
x - 1 = 0
⇔ x = 1
⇒ C(1; 0)
c) Gọi (t): y = ax + b (a 0)
Do (t) // (d) nên a = -2
⇒ (t): y = -2x + b
Thay y = -3 vào (d') ta có:
x - 1 = -3
⇔ x = -3 + 1
⇔ x = -2
Thay x = -2; y = -3 vào (t) ta có:
-2.(-2) + b = -3
⇔ 4 + b = -3
⇔ b = -3 - 4
⇔ b = -7
Vậy (t): y = -2x - 7

1.
để ............. căt nhau tại 1 điểm trên trục tung thì:
\(\hept{\begin{cases}0\ne2\left(T.m\right)\\2+m=3-m\end{cases}}\)
<=>2m=1
<=>m=1/2

Đáp án A.
Gọi M(x,y) là giao điểm của đồ thị (C) với trục tung.
Khi đó ta có x = 0 => y = -2.
Vậy M(0;-2)