Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7
= x7 - (3x2+ x2) – x5+ x4 + 2x – 7
= x7 – 4x2 – x5+ x4 + 2x – 7
= x7 – x5 + x4 – 4x2 + 2x - 7
g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1
= x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1
= x – 6x2 + x4 – x5 – x7 – 1
= -x7 – x5 + x4 – 6x2 + x – 1
* f(x) – g(x)
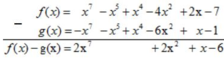
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6
* f(x) = x2 + 2x3− 7x5 − 9 − 6x7 + x3 + x2 + x5 − 4x2 + 3x7
= (x2+ x2 – 4x2)+ (2x3 + x3 ) - (7x5 - x5 ) – 9 – (6x7 – 3x7)
= - 2x2 + 3x3 – 6x5 – 9 – 3x7
Sắp xếp theo thứ tự tăng của biến: f(x) = −9 − 2x2 + 3x3 − 6x5 − 3x7
* g(x) = x5 + 2x3 − 5x8 − x7 + x3 + 4x2 -5x7 + x4 − 4x2 − x6 – 12
= x5+ (2x3 + x3) - 5x8 – (x7+ 5x7) + (4x2 – 4x2 ) + x4 – x6 – 12
= x5 + 3x3 – 5x8 – 6x7 + x4 – x6 – 12
Sắp xếp theo thứ tự tăng của biến: g(x) = −12 + 3x3 + x4 + x5 – x6 − 6x7− 5x8
* h(x) = x + 4x5 − 5x6 − x7 + 4x3 + x2 − 2x7 + x6 − 4x2 − 7x7 + x.
= (x+ x) +4x5 – (5x6 – x6)- (x7 + 2x7+ 7x7) + 4x3+ (x2 – 4x2)
= 2x + 4x5 - 4x6 – 10x7 + 4x3 -3x2
Sắp xếp theo thứ tự tăng của biến: h(x) = 2x − 3x2 + 4x3 + 4x5 − 4x6 − 10x7
Đáp án A
(c) ⇒ X3 là HOOC(CH2)4COOH, X4 là H2N(CH2)6NH2.
(d) ⇒ X2 là CH3OH, X5 là CH3COOH || (e) ⇒ X6 là C2H5OH.
⇒ X7 là C2H5OOC(CH2)4COOH ⇒ M = 174 g/mol
a: P(x)=4x^5-4x^5-2x^3+x^4-3x^2+4x^2+3x-5x+1
=x^4-2x^3+x^2-2x+1
Q(x)=x^7-x^7-2x^6+2x^6+2x^3-2x^4+2x^4+x^5-x^5-x+5
=2x^3-x+5
b: P(x)+Q(x)
=x^4-2x^3+x^2-2x+1+2x^3-x+5
=x^4+x^2-3x+6
P(x)-Q(x)
=x^4-2x^3+x^2-2x+1-2x^3+x-5
=x^4-4x^3+x^2-x-4
Thay x = 1 vào f(x) ta được
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
f(1)=1+13+15+17+…+1101
=1+1+1+…+1 =51.1 =51
Thay x = -1 vào f(x) ta được
f(−1)=1+(−1)3+(−1)5+(−1)7+…+(−1)101
=1+(−1)+(−1)+…+(−1)
=1+50.(−1)=1−50=−49
Thay x = 1 vào f(x) ta được
f ( 1 ) = 1 + 1 3 + 1 5 + 1 7 + … + 1 101 = 1 + 1 + 1 + … + 1 ⏟ 51501 = 51.1 = 51
Thay x = -1 vào f(x) ta được
f ( − 1 ) = 1 + ( − 1 ) 3 + ( − 1 ) 5 + ( − 1 ) 7 + … + ( − 1 ) 101 = 1 + ( − 1 ) + ( − 1 ) + … + ( − 1 ) ⏟ 50 : 0 ( − 1 ) = 1 + 50. ( − 1 ) = 1 − 50 = − 49 Vây f ( 1 ) = 51 ; f ( − 1 ) = − 49
Chọn đáp án B
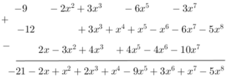
f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7
= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)
= 2x5 + x2 – 4x3.
= 2x5 - 4x3 + x2
Đa thức có bậc là 5
g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8
= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)
= 2x4 + 5x3 – 6x8 – 3x7 – 3x2
= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.
Đa thức có bậc là 8.
Đa thức có bậc là 5 nhe