Đo chiều cao của 100 học sinh lớp 6 (đơn vị đo: cm) và được kết quả theo bảng 26:
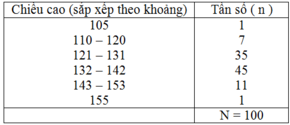
Ước tính số trung bình cộng trong trường hợp này.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
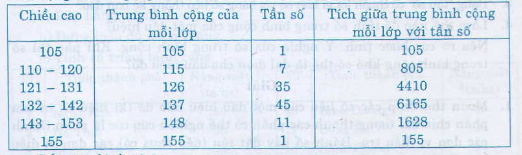
Số trung bình cộng:\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.

Số trung bình cộng:¯¯¯¯¯X=105+805+4410+6165+1628+155100=132,68(cm)

a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.

Số trung bình cộng:
\(\overline{X}=\dfrac{105+805+4410+6165+1628+155}{100}=132,68\left(cm\right)\)

Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.

Dấu hiệu ở đây là chiều cao của mỗi học sinh lớp 6A
Chọn đáp án B

a) Tính chiều cao trung bình của học sinh nam
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp :
\(\overline{x}=\dfrac{1}{60}\left(5.140+9.150+19.160+17.170+10.180\right)\)
\(\overline{x}=163\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(8,33.140+15.150+31,67.160+28,33.170+16,67.180\right)\)\(\overline{x}=163\)
Tính chiều cao trung bình của học sinh nữ:
Cách 1 : Sử dụng bảng phân bố tần số ghép lớp \(\overline{x}=\dfrac{1}{60}\left(8.140+15.150+16.160+14.170+7.180\right)\)
\(\overline{x}=159,5\)
Cách 2 : Sử dụng bảng phân bố tần suất ghép lớp :
\(\overline{x}=\dfrac{1}{100}\left(13,33.140+25.150+26,67.160+23,33.170+11,67.180\right)\)
\(\overline{x}=159,5\)
b) Vì \(\overline{x}_{nam}=163>\overline{x}_{nữ}=159,5\) nên suy ra học sinh ở nhóm nam cao hơn học sinh ở nhóm nữ
c) \(\overline{x}=\left(60.159,5+60.163\right)\dfrac{1}{2}\approx161\left(cm\right)\)

Giá trị trung bình các giá trị trong bảng là :
( 115 + 121 ) : 2 = 118
( 122 + 131 ) : 2 = 126, 5
( 132 + 141 ) : 2 = 136, 5
( 142 + 151 ) : 2 = 146, 5
Vậy ta có bảng mới như sau :
| Chiều cao | Tần số |
| 118 | 16 |
| 126, 5 | 22 |
| 136, 5 | 38 |
| 146, 5 | 24 |
X = \(\frac{118\cdot16+126,5\cdot22+136,5\cdot38+146,5\cdot24}{16+22+38+24}=\frac{13374}{100}=133,74\)
Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp: sau cột tần số là cột tích giữa trung bình cộng.
(Nếu có bạn thắc mắc là tại sao lại có được số liệu ở cột Trung bình cộng ở mỗi lớp. Đó là vì ta lấy tổng chiều cao đầu + chiều cao cuối của mỗi lớp, sau đó chia cho 2. Ví dụ: (110 + 120)/2 = 115)