Thu gọn biểu thức 343 a 3 b 6 - 125 3 ta được
A. - 7 ab 2 5
B. 7 ab 2 5
C. - ab 2 5
D. ab 2 5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
15 tháng 5 2017
Đúng(0)
ND
Nguyễn Đức Thịnh
17 tháng 3 2022
Dáp and là 1
Đúng(0)
Những câu hỏi liên quan
14 tháng 7 2021
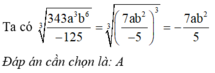
`(2-2/5+6/5)-(3/15+2)+(7/3-2)`
`=2+4/5-3/15-2-2+7/3`
`=-2+4/5-1/5+7/3`
`=-2+3/5+2+1/3`
`=3/5+1/3=14/15`
`=>a=14,b=15`
`=>S=2.14-15=13`
CM
11 tháng 2 2017
Ta có
B = 2 a − 3 a + 1 − a − 4 2 − a a + 7 = 2 a 2 + 2 a – 3 a – 3 – ( a 2 – 8 a + 16 ) – ( a 2 + 7 a ) = 2 a 2 + 2 a – 3 a – 3 – a 2 + 8 a – 16 – a 2 – 7 a = - 19
Đáp án cần chọn là: D
29 tháng 1
\(P=\dfrac{a^{\dfrac{1}{3}}\cdot\sqrt{b}+b^{\dfrac{1}{3}}\cdot\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}-\sqrt[3]{ab}\)
\(=\dfrac{a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{2}}+b^{\dfrac{1}{3}}\cdot a^{\dfrac{1}{2}}}{a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)
\(=\dfrac{a^{\dfrac{2}{6}}\cdot b^{\dfrac{3}{6}}+a^{\dfrac{3}{6}}\cdot b^{\dfrac{2}{6}}}{a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)
\(=\dfrac{a^{\dfrac{2}{6}}\cdot b^{\dfrac{2}{6}}\left(a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}\right)}{a^{\dfrac{1}{6}}+b^{\dfrac{1}{6}}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)
\(=a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}-a^{\dfrac{1}{3}}\cdot b^{\dfrac{1}{3}}\)
=0
6 tháng 3 2022
a: \(A=\dfrac{6}{7}x^2y^2\cdot\dfrac{-7}{2}x^2y=-3x^4y^3\)
b: Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{x}{-2}=\dfrac{y}{3}=\dfrac{x-y}{-2-3}=\dfrac{5}{-5}=-1\)
Do đó: x=2; y=-3
\(A=-3x^4y^3=-3\cdot2^4\cdot\left(-3\right)^3=3\cdot27\cdot16=81\cdot16=1296\)
6 tháng 3 2022
\(A=\dfrac{6}{7}x^2y^2.\left(-3\dfrac{1}{2}x^2y\right)\)
\(=\dfrac{6}{7}x^2y^2.\left(-\dfrac{7}{2}\right)x^2y\)
\(=-3x^4y^3\)
b)Có: \(\dfrac{x}{y}=-\dfrac{2}{3}\Leftrightarrow\dfrac{x}{2}=\dfrac{-y}{3}=\dfrac{x-y}{2+3}=\dfrac{5}{5}=1\)
\(\Rightarrow x=2;y=-3\)
Tại \(x=2;y=-3\) , giá trị của biểu thức là:
\(-3.2^4.\left(-3\right)^3=-3.16.\left(-27\right)=1296\)
7 tháng 4 2020
a) \(\frac{2^7\cdot9^3}{6^5\cdot8^2}=\frac{2^7\cdot\left(3^2\right)^3}{\left(2\cdot3\right)^5\cdot\left(2^3\right)^2}=\frac{2^7\cdot3^6}{2^5\cdot3^5\cdot2^6}=\frac{3}{2^4}=\frac{3}{16}\)
c) \(\frac{5^4\cdot20^4}{25^4\cdot4^5}=\frac{5^4\cdot\left(2^2\cdot5\right)^4}{\left(5^2\right)^4\cdot\left(2^2\right)^5}=\frac{5^4\cdot2^8\cdot5^4}{5^8\cdot2^{10}}=\frac{1}{2^2}=\frac{1}{4}\)
d) \(\frac{\left(5^4\cdot20^4\right)^3}{125^4}=\frac{5^{12}\cdot20^{12}}{\left(5^3\right)^4}=\frac{5^{12}\cdot\left(2^2\cdot5\right)^{12}}{5^{12}}=2^{24}\cdot5^{12}\)
20 tháng 5 2022
a: \(=\dfrac{2^6\cdot3^3}{3^{-4}\cdot2^6}=\dfrac{3^3}{3^{-4}}=3^7\)
c: \(=5^4\cdot5^3\cdot\left(\dfrac{5}{2}\right)^{-5}\cdot\dfrac{4}{100}\)
\(=5^7\cdot\left(\dfrac{2}{5}\right)^5\cdot\left(\dfrac{1}{5}\right)^2\)
\(=5^2\cdot\left(\dfrac{1}{5}\right)^2\cdot5^5\cdot\left(\dfrac{2}{5}\right)^5=2^5\)
H
2
9 tháng 8 2021
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
9 tháng 8 2021
Ta có:(a2+ab+b2)(a2-ab+b2)-(a4+b4)
= (a2+b2)2-a2b2-a4-b4=a4+2a2b2+b4-a2b2-a4-b4=a2b2
23 tháng 12 2023
Bài 1:
a: \(\sqrt{50}+2\sqrt{8}-\dfrac{3}{2}\cdot\sqrt{72}+\sqrt{125}\)
\(=5\sqrt{2}+2\cdot2\sqrt{2}-\dfrac{3}{2}\cdot6\sqrt{2}+\sqrt{125}\)
\(=9\sqrt{2}-9\sqrt{2}+5\sqrt{5}=5\sqrt{5}\)
b: \(\left(3\sqrt{2}-\sqrt{5}\right)^2-\dfrac{9}{\sqrt{5}-\sqrt{2}}\)
\(=18-2\cdot3\sqrt{2}\cdot\sqrt{5}+5-\dfrac{9\left(\sqrt{5}+\sqrt{2}\right)}{5-2}\)
\(=23-6\sqrt{10}-3\left(\sqrt{5}+\sqrt{2}\right)\)
\(=23-6\sqrt{10}-3\sqrt{5}-3\sqrt{2}\)
c: \(5\sqrt{4a}-3\sqrt{25a}+\sqrt{9a}\)
\(=5\cdot2\sqrt{a}-3\cdot5\sqrt{a}+3\sqrt{a}\)
\(=10\sqrt{a}-15\sqrt{a}+3\sqrt{a}=-2\sqrt{a}\)