Gọi S là diện tích của hình phẳng giới hạn bởi parabol y = x 2 2 và đường tròn có tâm tại gốc tọa độ, bán kính bằng 2 2 . Biết S = a π + b c , trong đó a , b , c ∈ ℕ * , b , c = 1 . Tính tổng a + b + c .
A. 6
B. 7
C. 8
D. 9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
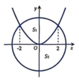
Phương trình đường tròn tâm O có bán kính R = 2 2 là x 2 + y 2 = 8 .
Ta có parabol và đường tròn như hình vẽ bên.
Giao điểm của parabol và đường tròn là nghiệm của hệ phương trình
x 2 + y 2 = 8 y = x 2 2 ⇔ x = ± 2 y = 2
Vì parabol và đường tròn đều đối xứng qua trục Oy nên ta có
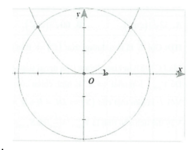
S = 2 ∫ 0 2 8 - x 2 - x 2 2 d x .
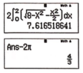
Bấm máy tính, ta được kết quả như hình bên. Ta biết S = a π + b c nên ta thao tác tiếp theo trên máy như hình bên.
Vậy ta có S = 2 π + 4 3 . Do đó ta có a = 2 , b = 4 , c = 3 ⇒ a + b + c = 9 . Chọn đáp án D.

Gọi ![]() là điểm tiếp xúc của (C), (P) nằm bên phải trục tung. Phương trình tiếp tuyến của (P) tại điểmA là
là điểm tiếp xúc của (C), (P) nằm bên phải trục tung. Phương trình tiếp tuyến của (P) tại điểmA là ![]() Vì (C), (P) tiếp xúc với nhau tại A nên tA là tiếp tuyến chung tại A của cả (C), (P). Do đó
Vì (C), (P) tiếp xúc với nhau tại A nên tA là tiếp tuyến chung tại A của cả (C), (P). Do đó ![]()
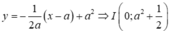
Vì 
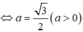
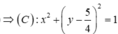
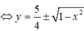
Diện tích hình phẳng cần tính bằng diện tích hình phẳng giới hạn bởi

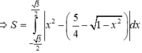
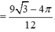
Chọn đáp án D.


Diện tích phần giới hạn giữa đường tròn và parabol là:
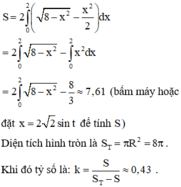
Chọn A.

Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3

Đáp án A
Phương pháp:
Tính khoảng cách từ 1 điểm M đến đường thẳng
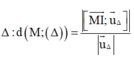
![]()
là 1 điểm bất kì
Cách giải:
![]()
là một VTCP
![]()
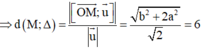
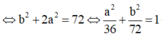
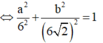
Như vậy tập hợp các điểm M là elip có phương trình
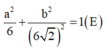
![]()
Đáp án D.