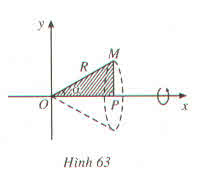
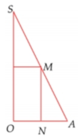
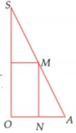
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox, cạnh huyền OM không đổi, O M = R ( R>0 ). Tính theo R giá trị lớn nhất của thể tích khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox.
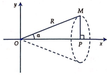
A. 2 3 π R 3 27
B. 2 3 π R 3 9
C. 2 2 π R 3 27
D. 2 2 π R 3 9

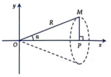

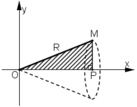

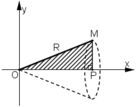
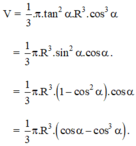
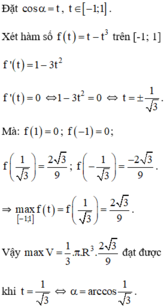
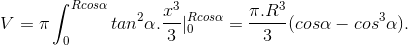
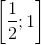 . (vì α ∈
. (vì α ∈ 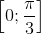 ), α = arccos t.
), α = arccos t.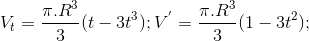
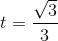
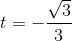 (loại).
(loại).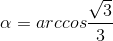 .
.



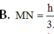

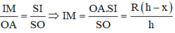
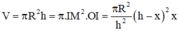
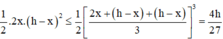
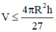 .
. 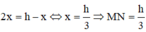
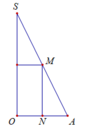
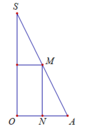
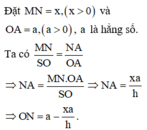
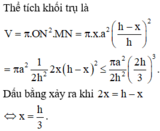
Đáp án A.