Tổng tất cả các nghiệm của phương trình cos5x + cos2x + 2sin3x.sin2x = 0 trên 0 ; 2 π là
A. 3 π
B. 4 π
C. 5 π
D. 6 π
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Phương trình ![]()
![]()
Xét hàm số f(t) = 2017t + t ; ta có f’(t) = 2017tln2017 + 1 > 0 mọi x
Suy ra hàm số đồng biến trên R.
Nhận thấy (*) có dạng f( sin2x) = f(cos2x) ; do đó: sin2x = cos2x
![]()
Vì 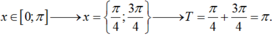

ĐKXĐ: \(cosx\ne-\dfrac{\sqrt{3}}{2}\) \(\Rightarrow\left[{}\begin{matrix}x\ne\dfrac{5\pi}{6}+k2\pi\\x\ne\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(pt\Rightarrow3-\left(1-2sin^2x\right)+2sinx.cosx-5sinx-cosx=0\)
\(\Leftrightarrow2sin^2x-5sinx+2+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx-2\right)+cosx\left(2sinx-1\right)=0\)
\(\Leftrightarrow\left(2sinx-1\right)\left(sinx+cosx-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\dfrac{1}{2}\\sinx+cosx=2\left(vn\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k2\pi\\x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Loại nghiệm
\(\Rightarrow x=\dfrac{\pi}{6}+k2\pi\)
\(0\le\dfrac{\pi}{6}+k2\pi\le2022\pi\Rightarrow0\le k\le1010\)
\(\Rightarrow\sum x=1011.\dfrac{\pi}{6}+2\pi\left(0+1+2+...+1010\right)=\dfrac{1011\pi}{6}+2\pi.\dfrac{1010.1011}{2}=...\)
Hướng dẫn giải:
Chọn A
Ta có: cos5x + cos2x + 2sin3x. sin2x =0
<=> cos 5x + cos2x - cos5x + cosx = 0
<=> cos2x + cosx = 0 <=> 2cos2x – 1 + cosx =0