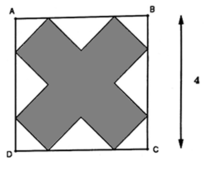
Từ một hình vuông người ta cắt các tam giác vuông cân tạo ra hình bôi đậm như hình vẽ. Sau đó họ lại gập lại thành một hình hộp chữ nhật không nắp. Tính diện tích lớn nhất của hình hộp này
A. 30 3
B. 34 3
C. 32 3
D. 16
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi chiều rộng của hình chữ nhật ban đầu là x(cm), 0<x<18.
⇒ Chiều dài của hình chữ nhật ban đầu là 18-x (cm)
Hình hộp tạo thành có chiều dài là 18-x-6 = 12-x (cm), chiều rộng là x-6 (cm) và chiều cao là 3(cm). Do đó thể tích của hình hộp là


Đáp án B
Gọi chiều rộng của hình chữ nhật ban đầu là x (cm), 0 < x < 18
=> Chiều dài của hình chữ nhật ban đầu là 18 - x(cm)
Hình hộp tạo thành có chiều dài là 18 - x - 6 = 12 - x(cm), chiều rộng là x - 6 (cm) và chiều cao là (3cm). Do thể tích của hình hộp là

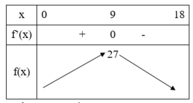
Từ bảng biến thiên suy ra thể tích lớn nhất ![]()

Chọn D
Hình hộp có đáy là hình vuông cạnh: 12 - 2x
Chiều cao của hình hộp là: x
Thể tích hình hộp là y = x ( 12 - 2 x ) 2
Bài toán đưa về tìm x ∈ (0; 6) để hàm số y = f ( x ) = x ( 12 - 2 x ) 2 có giá trị lớn nhất.
y ' = 1 ( 12 - 2 x ) 2 + x . 2 . ( 12 - 2 x ) . ( - 2 )
12 x 2 - 96 x + 144 ;
y' xác định ∀ x ∈ (0; 6)
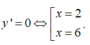
Bảng biến thiên
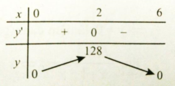
Hàm số đạt giá trị lớn nhất tại x=2

a) Độ dài cạnh mỗi hình vuông đã cắt hay chiều cao của cái hộp đó là : 4cm ( vì \(4\times4=16\))
Chiều rộng của cái hộp đó là :
\(20-4\times2=12\left(cm\right)\)
Chiều dài của cái hộp đó là :
\(30-4\times2=22\left(cm\right)\)
b) Diện tích xung quanh của cái hộp đó là :
\(\left(22+12\right)\times2\times4=272\left(cm^2\right)\)
Diện tích đáy của cái hộp đó là :
\(22\times12=264\left(cm^2\right)\)
Tổng diện tích 5 mặt của cái hộp đó là :
\(272+264=536\left(cm^2\right)\)
Đáp số : a) Chiều dài 22cm ; chiều rộng 12cm ; chiều cao 4cm
b) 536cm\(^2\)
Đáp án C