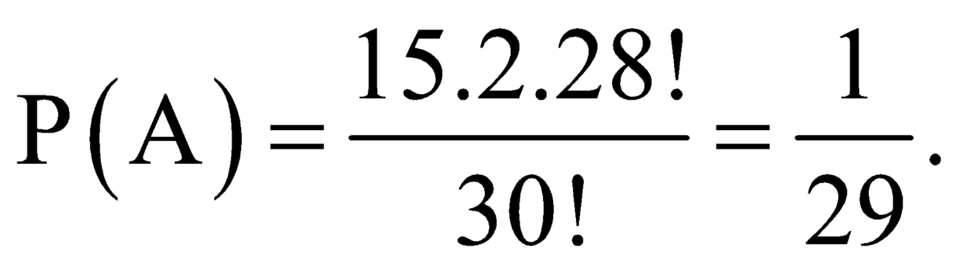Một phòng học có 15 bộ bàn ghế, xếp chỗ ngồi cho 30 học sinh, mỗi bàn ghế 2 học sinh. Tìm xác suất để hai học sinh A, B chỉ định trước ngồi cùng một bàn.
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Số phẩn tử không gian mẫu là | Ω | = 30 !
Gọi A là biến cố “Hai học sinh A, B ngồi cạnh nhau”.
Chọn 1 bàn để xếp hai học sinh A, B có 15 cách.
Xếp A, B ngổi vào bàn được chọn có 2! cách.
Xếp 28 học sinh còn lại có 28! cách.
Vậy | Ω A | = 15 . 2 . 28 ! . Do đó P ( A ) = 15 . 2 . 28 ! 30 ! = 1 29 .

Lời giải:
Giả sử trong phòng học có $a$ học sinh.
Theo bài ra, nếu xếp mỗi bộ bàn ghế 3 hs thì số bộ bàn ghế là:
$\frac{a-4}{3}$ (bộ)
Nếu xếp mỗi bộ bàn ghế 4 học sinh thì số bộ bàn ghế là:
$\frac{a-2}{4}$ (bộ)
Số bộ bàn ghế không đổi nên: $\frac{a-4}{3}=\frac{a-2}{4}$
$\Rightarrow a=10$ (hs)
Số bộ bàn ghế là: $\frac{a-2}{4}=\frac{10-2}{4}=2$ (bộ)

Số học sinh một phòng học có thể chứa là:
11×4=44(học sinh)
Số học sinh trường có thể nhận nhiều nhất là:
44×50=2200(học sinh)
Đ/s: 2200 học sinh
Số bộ bàn ghế là \(11\times50=550\left(bộ\right)\)
Vậy trường nhận được nhiều nhất \(550\times4=2200\left(hs\right)\)

Tổng số bộ bàn ghế là:
\(11\cdot50=550\) (bộ)
Tổng số chỗ ngồi là:
\(550\cdot4=2200\) (chỗ ngồi)
Vậy trường có thể nhận được nhiều nhất 2200 học sinh

a) Mỗi bàn học có số bộ bàn ghế là
255 : 17=15 (bộ bàn ghế )
b) Số bộ bàn ghế có 1 học sinh ngồi là:
15 : 3x1=5( bộ bàn ghế)
Số bộ bàn ghế có 2 học sinh ngồi là:
15 - 5 = 10 (học sinh)
Vậy mỗi lớp có số học sinh là
(10x 2)+ (5x1)=25 (học sinh)
Vậy trường đó có số học sinh là:
25 x 17=425 (học sinh)
Đáp số: 425 học sinh
mình chỉ giải được phần a} thôi bạn thông cảm cho mình nhé !
mỗi phòng có số bộ bàn ghế là :
255 : 17 = 15 ( bộ )
vậy mỗi phòng có 15 bộ bàn ghế ^^ }

Moi phong co so hoc sinh la
2*15=30 ( hs )
Co tat ca so hoc sinh dang ngoi hoc la
30*8=240 (hs)
dap so 240 hoc sinh

Số học sinh đang ngồi học là:
(15×2)×5=150 (học sinh)
Đáp số: 150 học sinh.
Đáp án D
Đáp án B
Số phẩn tử không gian mẫu là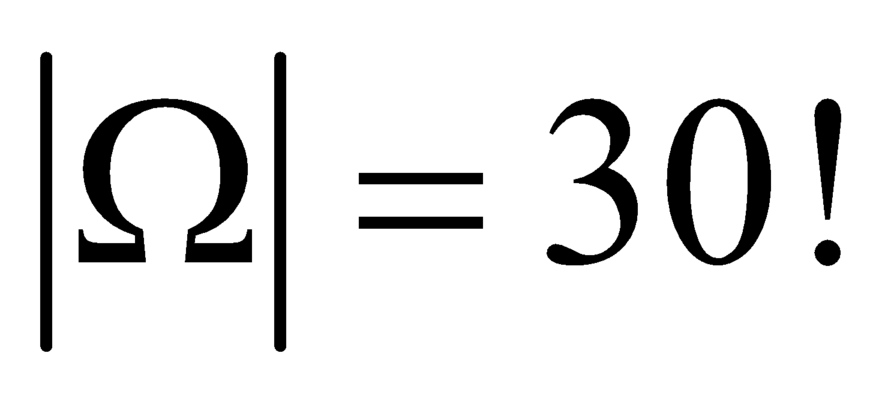
Gọi A là biến cố “Hai học sinh A, B ngồi cạnh nhau”.
Chọn 1 bàn để xếp hai học sinh A, B có 15 cách.
Xếp A, B ngổi vào bàn được chọn có 2! cách.
Xếp 28 học sinh còn lại có 28! cách.
Vậy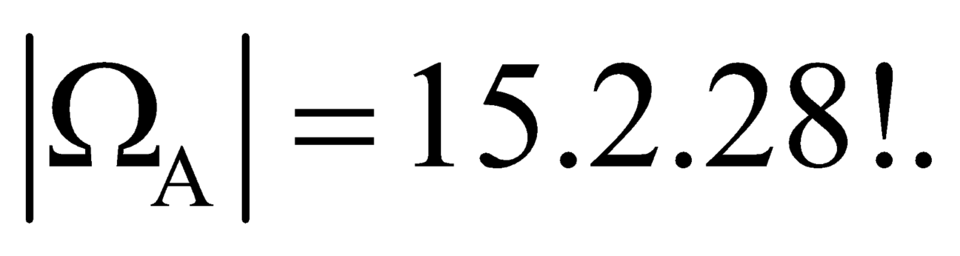
Do đó