Cho hai dãy ghế được xếp như sau : Xếp 4 bạn nam và 4 bạn nữ vào hai dãy ghế trên. Hai người được gọi là ngồi đối diện với nhau nếu ngồi ở hai dãy và có cùng vị trí ghế (số ở ghế). Số cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ bằng A. 4!4!24 B. 4!4! C. 4!.2 D....
Đọc tiếp
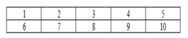
Cho hai dãy ghế được xếp như sau :
Xếp 4 bạn nam và 4 bạn nữ vào hai dãy ghế trên. Hai người được gọi là ngồi đối diện với nhau nếu ngồi ở hai dãy và có cùng vị trí ghế (số ở ghế). Số cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ bằng
A. 4!4!24
B. 4!4!
C. 4!.2
D. 4!4!.2
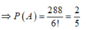
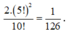
Đáp án A
Phương pháp :
+) Chọn vị trí cho các bạn nam (hoặc nữ).
+) Hoán đổi các vị trí.
+) Sử dụng quy tắc nhân.
Cách giải : Chọn 1 vị trí trong 2 vị trí đối xứng có C 2 1 cách chọn, như vậy có ( C 2 1 ) 4 = 2 4 cách chọn ghế cho 4 bạn nam.
4 bạn nam này có thể đổi chỗ cho nhau nên có 4! cách xếp
Vậy có 4!4!24 cách xếp để mỗi bạn nam ngồi đối diện với một bạn nữ.