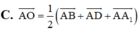
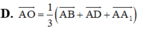
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
- Phương pháp: Sử dụng công thức ba điểm và công thức hình bình hành
- Cách giải:
+ Do A B C D . A 1 B 1 C 1 D 1 là hình lập phương nên A C C 1 A 1 là hình chữ nhật.
⇒ O là trung điểm của AC1
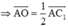
+ Ta có:
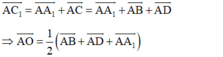
Đáp án C
Ta có A O → = 1 2 A A 1 → + A C → = 1 2 A A 1 → A B → + A D →
Gọi M, N lần lượt là trung điểm các cạnh A′B′,C′D′ ta có ((OA′B′), (OC′D′)) = (OM,ON).
Ta có
MN=a,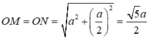 
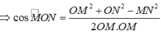
= 3 5
Chọn đáp án D.
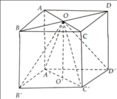
a) Bốn tam giác OAA', OBB', OCC', ODD' là các tam giác vuông bằng nhau nên suy ra OA' = OB' = OC' = OD'.
Hình chóp O.A'B'C'D' là hình chóp đều vì có các mặt bên là tam giác cân và đáy là đa giác đều.
b) Thể tích của của hình chóp O.A'B'C'D' là:
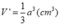
Thể tích hình lập phương:
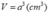
Vậy V ' V = 1 3
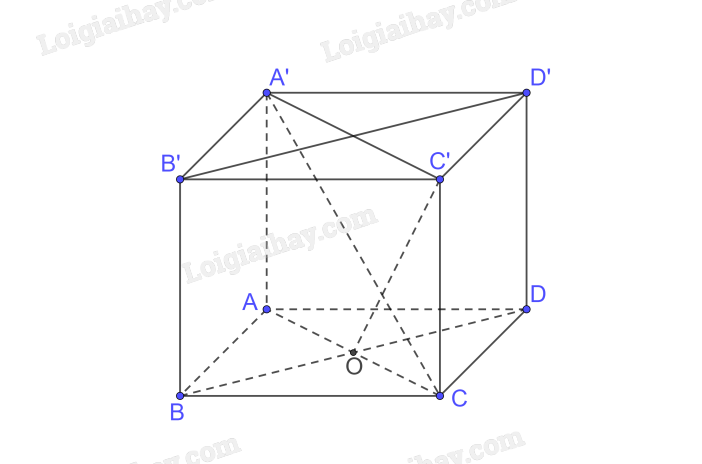
a) Xét tam giác ABC vuông tại B có
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \)
Xét tam giác AA’C vuông tại A có
\(A'{C^2} = A{A'^2} + A{C^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow A'C = a\sqrt 3 \)
Vậy độ dài đường chéo hình lập phương bằng \(a\sqrt 3 \)
b) Ta có \(\begin{array}{l}BD \bot AC,BD \bot AA' \Rightarrow BD \bot \left( {ACC'A'} \right);BD \subset \left( {BDD'B'} \right)\\ \Rightarrow \left( {ACC'A'} \right) \bot \left( {BDD'B'} \right)\end{array}\)
c) Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),CO \bot BD \Rightarrow \left[ {C,BD,C'} \right] = \left( {CO,C'O} \right) = \widehat {COC'}\)
\(OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác COC’ vuông tại C có
\(\tan \widehat {COC'} = \frac{{CC'}}{{OC}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 \Rightarrow \widehat {COC'} = \arctan \sqrt 2 \)
Ta có \(C'O \bot BD\left( {BD \bot \left( {ACC'A'} \right)} \right),AO \bot BD \Rightarrow \left[ {A,BD,C'} \right] = \left( {AO,C'O} \right) = \widehat {AOC'}\)
\(\widehat {AOC'} = {180^0} - \widehat {COC'} \approx 125,{26^0}\)
