Cho hàm số y = f(x) xác định trên
R
/
-
1
, liên tục trên mỗi khoảng xác định và có bảng biến thiên: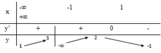
Hỏi khẳng định nào dưới đây là khẳng định sai?
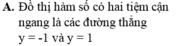

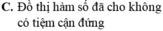
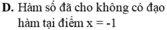
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
Vì hàm số không xác định tại x=-1 nên hàm số đồng biến trên ( - ∞ ; - 1 ) ; ( - 1 ; 1 ) .

Đáp án D.
Quan sát bảng biến thiên, ta thấy:
lim x → − 1 − y = + ∞ ; lim x → − 1 + y = − ∞ lim x → 1 − y = − ∞ ; lim x → 1 + y = − ∞ → Đồ thị hàm số có hai đường tiệm cận đứng là x = − 1 và x = 1 . A đúng.
lim x → − ∞ y = 3 ; lim x → + ∞ y = 3 → Đồ thị hàm số có tiệm cận ngang là đường thẳng . B đúng.
Hàm số không có đạo hàm tại điểm , tuy nhiên vẫn đạt giá trị cực đại y=2 tại x=0 . C đúng.
Hàm số không đạt cực trị tại điểm x=1 . D sai.
Cách 1: Tư duy tự luận
Do π > 1 nên π a > π = π 1 ⇔ a > 1 . Vậy A đúng.
Do a > 1 nên a 5 < a 3 ⇔ 5 < 3 (hiển nhiên). Vậy B đúng.
Do e > 1 nên e a > 1 ⇔ e 0 ⇔ a > 0 . Vậy C đúng.
Do a > 1 nên a − 3 > a 2 ⇔ − 3 > 2 (vô lý). Vậy D sai.
Cách 2: Sử dụng máy tính cầm tay
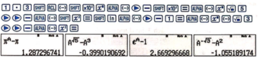
Như vậy nếu a > 1 thì a − 3 < a 2 . Đáp án D sai.

Dựa vào bảng biến thiên nhận thấy hàm số đồng biến trên các khoảng - ∞ ; - 1 và (-1;1)
Vì vậy khẳng đinh C là sai. Chọn C.

Đáp án D
Tại -1 hàm số không xác định nên không nghịch biến trên ( - ∞ ; 3 )

Đáp án A.
Điểm M(0; 2) được gọi là điểm cực đại của đồ thị hàm số.