Với mỗi x > 2, trong các biểu thức: 2 x

PT

Pham Trong Bach

12 tháng 9 2017

Với mỗi x > 2, trong các biểu thức: 2 x ; 2 x + 1 ; 2 x - 1 ; x + 1 2 ; x 2 giá trị...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

12 tháng 9 2017

Đúng(0)

PT

Pham Trong Bach

18 tháng 2 2017

Với mỗi x > 2, trong các biểu thức: 2 x , 2 x + 1 , 2 x - 1 , x + 1 2 , x 2 giá trị biểu thức nào là nhỏ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

18 tháng 2 2017

Đáp án B

Đúng(0)

DK

Đỗ Kiều Giang

25 tháng 12 2018 - olm

cho biểu thức A= $\frac{\sqrt{x}-2}{\sqrt{x}}$với x>0

1 Tính giá trị biểu thức A khi x=16

2 Rút gọn biểu thức P=A.$\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right)$với x>0, x khác 4

3 Tìm các giá trị x để P>$\frac{1}{3}$

#Toán lớp 9

0

QP

Quang Phạm

10 tháng 2 2019 - olm

tính giá trị nhỏ nhất của biểu thức P=x^2-x+1/x^2+x+1 với các giá trị của x>0

#Toán lớp 8

8

TT

Trần Thanh Phương

10 tháng 2 2019

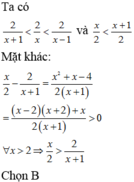
P/s: ko chắc

$P=\frac{x^2-x+1}{x^2+x+1}$

$P=\frac{x^2}{x^2+x+1}-\frac{x}{x^2+x+1}+\frac{1}{x^2+x+1}$

$P=x^2\cdot\frac{1}{x^2+x+1}-x\cdot\frac{1}{x^2+x+1}+\frac{1}{x^2+x+1}$

$P=\frac{1}{x^2+x+1}\left(x^2-x+1\right)$

$P=\frac{1}{x^2+x+1}\left[x^2-2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{3}{4}\right]$

$P=\frac{1}{x^2+x+1}\left[\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\right]$

$P=\frac{1}{x^2+x+1}\cdot\left(x-\frac{1}{2}\right)^2+\frac{1}{x^2+x+1}\cdot\frac{3}{4}$

Vì $\frac{1}{x^2+x+1}\cdot\left(x-\frac{1}{2}\right)^2\ge0\forall x$

$\Rightarrow P\ge\frac{1}{x^2+x+1}\cdot\frac{3}{4}$

Dấu "=" xảy ra $\Leftrightarrow\frac{1}{x^2+x+1}\cdot\left(x-\frac{1}{2}\right)^2\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

Vậy...

Đúng(0)

TT

Thanh Tùng DZ

10 tháng 2 2019

dễ hơn nè

Ta thấy x² + x + 1 > 0

Ta có : 2 ( x - 1 )² $\ge$0 $\Rightarrow$2x² - 4x + 2 $\ge$0 $\Rightarrow$3 ( x² - x + 1 ) $\ge$x² + x + 1

$\Rightarrow\frac{x^2-x+1}{x^2+x+1}\ge\frac{1}{3}$ . Dấu " = " xảy ra $\Leftrightarrow$x = 1

Đúng(0)

KK

Kim Khánh Linh

15 tháng 5 2021 - olm

Cho hai biểu thức: $A=\dfrac{\sqrt{x}}{\sqrt{x}+2}$ và $B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}$ với $x>0$ và $x \neq 4$

1) Tính giá trị của biểu thức $A$ khi $x=9$.

2) Rút gọn biểu thức $B$.

3) Chứng minh: $\dfrac{A}{B}>-1$, với $x>0$ và $x \neq 4$.

#Toán lớp 9

2

B

Bellion

15 tháng 5 2021

Bài làm :

1) Khi x=9 ; giá trị của A là :

$A=\frac{\sqrt{9}}{\sqrt{9}+2}=\frac{3}{3+2}=\frac{3}{5}$

2) Ta có :

$B=...$

$=\frac{x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\frac{1.\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x+2}\right)}$

$=\frac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$=\frac{x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}$

$=\frac{\sqrt{x}}{\sqrt{x}-2}$

3) Ta có :

$\frac{A}{B}=\frac{\sqrt{x}}{\sqrt{x}+2}\div\frac{\sqrt{x}}{\sqrt{x}-2}=\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\sqrt{x}}=\frac{\sqrt{x}-2}{\sqrt{x}+2}=\frac{\sqrt{x}+2-4}{\sqrt{x}+2}=1-\frac{4}{\sqrt{x}+2}$

Xét :

$\frac{A}{B}+1=\frac{4}{\sqrt{x+2}}>0\Rightarrow\frac{A}{B}>-1$

=> Điều phải chứng minh

Đúng(0)

PT

Phùng Thị Uyên

4 tháng 6 2021

1, thay x=9(TMĐKXĐ) vào A ta đk:

A=$\dfrac{\sqrt{9}}{\sqrt{9}-2}=3$

vậy khi x=9 thì A =3

2,với x>0,x≠4 ta đk:

B=$\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}$

vậy B=$\dfrac{\sqrt{x}}{\sqrt{x}-2}$

3,$\dfrac{A}{B}>-1$ (x>0,x≠4)

⇒$\dfrac{\sqrt{x}}{\sqrt{x}+2}:\dfrac{\sqrt{x}}{\sqrt{x}-2}>-1\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}+2}.\dfrac{\sqrt{x}-2}{\sqrt{x}}>-1\Leftrightarrow\dfrac{\sqrt{x}-2}{\sqrt{x}+2}>-1$

⇒$\sqrt{x}-2>-1$ (vì $\sqrt{x}+2>0$)

⇔$\sqrt{x}>1$⇔x=1 (TM)

vậy x=1 thì $\dfrac{A}{B}>-1$ với x>0 và x≠4

Đúng(0)

NN

Nguyễn Ngọc Mai Anh

27 tháng 5 2017 - olm

1. tính gt biểu thứca)A=x(x2-y)-x2(x+y)+y(x2-x) với x=1/2; y=-100b) B=(x2-5)(x+3)+(x+4)(x-x2) với x=-12. chứng tỏ rằng gt mỗi biểu thức sau k phụ thuộc vào gt của biếna)x(x3-x2-3x+2)-(x2-2)(x2+x+3)+4(x2-x-2)b)(xn+1)(xn-2)-xn-3(xn+3-x3)+2017giúp mk với mk cần...

Đọc tiếp

#Toán lớp 8

3

ID

iam deadpool

27 tháng 5 2017

minh chua co luot k nao k minh di

Đúng(0)

TM

Trà My

28 tháng 5 2017

Bài 1:

a)$A=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)$$=x^3-xy-x^3-x^2y+yx^2-yx=-2xy$

Thay x=1/2 và y=-100 vào biểu thức A ta được $A=-2.\frac{1}{2}.\left(-100\right)=100$

b)$B=\left(x^2-5\right)\left(x+3\right)+\left(x+4\right)\left(x-x^2\right)=x^3+3x^2-5x-15-x^3-3x^2+4x$=-x-15

Thay x=-1 vào biểu thức B ta được B=-(-1)-15=1-15=-14

Đúng(0)

TP

Tài Phan

4 tháng 4 2016 - olm

Rút Gọn biểu thức

( x/(x^2-x) - (x-1)/(3x^2-4x-15)) chia (x^4-2x^2+1)/(3x^2+11x+10)*(x^-2x+1)

b, Tìm giá trị của biểu thức trên với x>0 , thỏa mãn |2x-3|+|x-1|=6005

c, chứng minh biểu thức trên >0 với mọi x>3

Ai giúp với ạ

#Toán lớp 8

0

NN

Nguyễn Ngọc Linh

19 tháng 1 2019 - olm

A=$\frac{x^2-25y^2}{x^2+y^2}\cdot\left(\frac{5x+y}{x^2-5xy}+\frac{5x-y}{x^2+5xy}\right)$

a, Tìm đkxđ của x để giá trị của biểu thức A được xác định

b,rút gọn biểu thức A

c,tính gt của A với x=-2,y=2010

d, tìm các gt của biến để A có gt bằng -2

#Toán lớp 8

0

CD

Cỏ dại

9 tháng 6 2019 - olm

Rút gọn các biểu thức :

$\frac{\sqrt{x^2}+\sqrt{4-4x+x^2+1}}{2x-1}$ với x > 2.

#Toán lớp 9

1

G

ღᏠᎮღ🆃🆄ấ🅽ঔ 🅽🅰🅼ঌ❄๖ۣۜ

9 tháng 6 2019

$\frac{\sqrt{x^2}+\sqrt{4-4x+x^2+1}}{2x-1}$

$=\frac{x+2-2\sqrt{x}+1}{2x-1}$

$=1+\frac{4-2\sqrt{x}}{2x-1}$

em lớp 8 chỉ làm được thế thôi

Đúng(0)

B

❤️ buồn ❤️

27 tháng 3 2020 - olm

cho biểu thức A=(x+3/x-2+x+2/3-x+x+2/x^2-5x+6):(1-x/x+1)

a.rút gọn biểu thức A

b.tính giá trị của x,biết A>1

c.tìm tất cả các giá trị nguyên của x để biểu thức B=3.A nhận giá trị là một số nguyên

d Khi x>2,tìm giá trị nhỏ nhất của biểu thức C=A.x

#Toán lớp 8

1

NK

Nguyễn Khánh Băng

28 tháng 3 2020

a) $\left(\frac{x+3}{x-2}+\frac{x+2}{3-x}+\frac{x+2}{x^2-5x+6}\right):\left(\frac{1-x}{x+1}\right)$

= $\left(\frac{x+3}{x-2}-\frac{x+2}{x-3}+\frac{x+2}{x^2-2x-3x+6}\right):\left(\frac{1-x}{x+1}\right)$

= $\left(\frac{\left(x+3\right)\left(x-3\right)}{\left(x-2\right)\left(x-3\right)}-\frac{\left(x+2\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)}+\frac{x+2}{\left(x-2\right)\left(x-3\right)}\right):\left(\frac{1-x}{x+1}\right)$

= $\left(\frac{x^2-9-x^2+4+x+2}{\left(x-2\right)\left(x-3\right)}\right).\frac{x+1}{1-x}$

=$\frac{-3+x}{\left(x-2\right)\left(x-3\right)}.\frac{x+1}{1-x}$

=$\frac{1}{\left(x-2\right)}.\frac{x+1}{1-x}$

=$\frac{x+1}{\left(x-2\right)\left(1-x\right)}$

b) Để A >1 $\Leftrightarrow\frac{x+1}{\left(x-2\right)\left(1-x\right)}>1$

$\Leftrightarrow\frac{-\left(1-x\right)\left(3-x\right)}{\left(x-2\right)\left(1-x\right)}$

$\Leftrightarrow\frac{x-3}{x-2}>0$

$\Rightarrow\orbr{\begin{cases}x-3\ge0\\x-2>0\end{cases}\Leftrightarrow\orbr{\begin{cases}x\ge3\\x>2\end{cases}\Leftrightarrow}x\ge3}$

$\Rightarrow\orbr{\begin{cases}x-3< 0\\x-2< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}x< 3\\x< 2\end{cases}\Leftrightarrow}x< 2}$

Vậy ...

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP