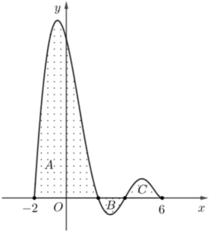
Cho hàm số liên tục trên đoạn [-2;6] và có đồ thị như hình vẽ. Biết rằng diện tích các hình phẳng
A, B, C trong hình vẽ lần lượt bằng 32; 2; 3. Tích phân ∫ - 2 2 ( f ( 2 x + 2 + 1 ) d x bằng
A. 22,5
B. 19,5
C. 37
D. 20,5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 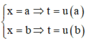
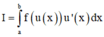


Chọn B.
Ta có: D = (-∞; -2] ∪ [2; +∞).
![]() .và f(2) = 0.
.và f(2) = 0.
Vậy hàm số liên tục tại x = 2.
Với -2 < x < 2 thì hàm số không xác định.

![]()
![]()
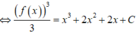
![]()
![]()
![]()
![]()
Xét hàm f x = 3 x 2 + 6 x 2 + 6 x + 1 3 trên - 2 ; 1
Ta có
![]()
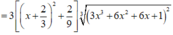
Nhận thấy f ' x > 0 , ∀ x ∈ ℝ
⇒ Hàm số đồng biến trên - 2 ; 1
Suy ra m a x [ - 2 , 1 ] f x = f 1 = 16 3
Chọn C

Ta có
![]()
![]()
![]()
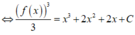
![]()
Ta có: f ( 0 ) = 1 ⇒ 1 = 3 C
![]()
![]()
Xét hàm ![]() trên [-2;1]
trên [-2;1]
Ta có
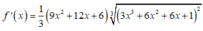
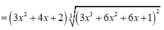
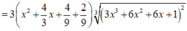
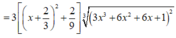
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒ Hàm số đồng biến trên (-2;1)
Suy ra m a x - 2 ; 1 f ( x ) = f ( 1 ) = 16 3
Chọn đáp án C.

Đáp án D.
Phương pháp:
∫ f " x . f ' x d x = f n + 1 x n + 1 + C , n ≠ − 1
Cách giải:
Ta có:
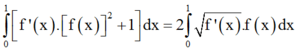
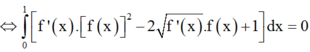


![]()
(do f x và f ' x đều nhận giá trị dương trên đoạn 0 ; 1 )


Mà
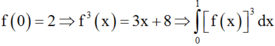

= 1 3 121 2 − 2 = 1 3 . 117 2 = 19 2
Chọn đáp án D.