Viết phương trình tiếp diện của mặt cầu S : x 2 + y 2 + z 2 + 2 x - 4 y - 6 z + 5 = 0 , biết tiếp diện song song với mặt phẳng ( P ) : x + 2 y - 2 z - 1 = 0 .
A. x + 2 y - 2 z + 6 = 0 v à x + 2 y – 2 z - 12 = 0
B. x + 2 y - 2 z - 6 = 0 v à x + 2 y – 2 z + 12 = 0
C. x + 2 y - 2 z + 4 = 0 v à x + 2 y – 2 z - 10 = 0
D. x + 2 y - 2 z - 4 = 0 v à x + 2 y – 2 z + 10 = 0







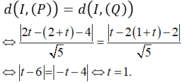
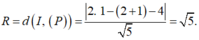

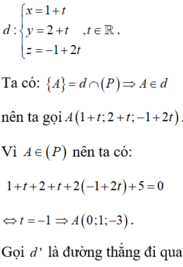
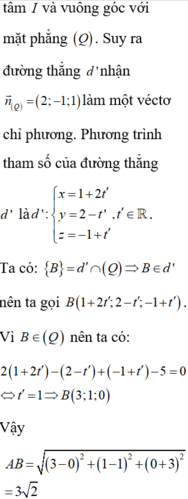
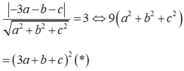
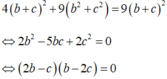
Chọn B.
Mặt cầu (S) tâm I(-1;2;3) và
Do mặt phẳng (α)//(P) nên (α) có dạng : x + 2y - 2z + m = 0.
Do (α) tiếp xúc với (S) ⇔ d(I,(α)) = R.
* Với m = - 6 suy ra mặt phẳng có phương trình: x + 2y - 2z - 6 = 0.
* Với m = 12 suy ra mặt phẳng có phương trình: x + 2y - 2z + 12 = 0.