Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y+1)²+ (z-2)²= 16 và điểm A (1;2;3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó. A. 10π. B. 38 π C. 33 π D. 36...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S): (x-1)²+ (y+1)²+ (z-2)²= 16 và điểm A (1;2;3). Ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu theo ba đường tròn. Tính tổng diện tích của ba đường tròn tương ứng đó.
A. 10π.
B. 38 π
C. 33 π
D. 36 π
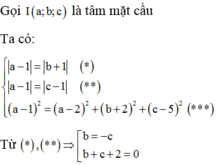
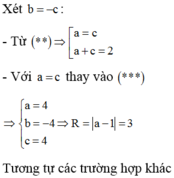
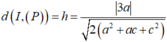
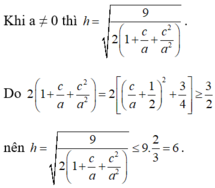
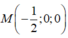
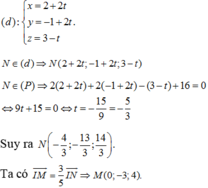
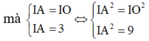
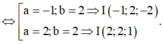
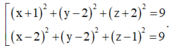
Cho ba mặt phẳng đôi một vuông góc với nhau (P), (Q), (R) tại I. Hạ AH, AD, AE lần lượt vuông góc với ba mặt phẳng trên thì ta luôn có: IA²=AD²+AH²+AE².
Chứng minh:
Chọn hệ trục tọa độ với I (0;0;0), ba trục Ox, Oy, Oz lần lượt là ba giao tuyến của ba mặt phẳng (P), (Q), (R).
Khi đó A (a, b, c) thì IA²=a²+b²+c²=d² (A, (Iyz))+d² (A, (Ixz))+d² (A, (Ixy)) hay IA²=AD²+AH²+AE² #đpcm~.
Áp dụng:
Mặt cầu (S) có tâm I (1;-1;2) và có bán kính r=4 ;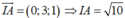
Gọi và ri là tâm và bán kính của các đường tròn I = 1;2;3
Ta có tổng diện tích các đường tròn là