Cho cơ hệ như hình vẽ, dây nhẹ không dãn, ròng rọc nhẹ không ma sát, m 1 trượt không ma sát trên mặt phẳng ngang, m 2 có trọng lượng 80N. Khi thế năng của hệ thay đổi lượng 64J thì m 1 đã đi được.
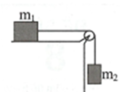
A. 8 m
B. 4 m
C. 0,8 m
D. Không tính được
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Chia chuyển động của hệ làm hai giai đoạn:
- Giai đoạn 1: Từ khi thả nhẹ cho hệ bắt đầu chuyển động đến lúc lò xo nén cực đại lần thứ nhất:
+ Các lực tác dụng lên M: lực căng dây T → và lực ma sát F m s → .
+ Các lực tác dụng lên m: lực đàn hồi F d h → và lực ma sát f m s → . Chuyển động của m là dao động điều hòa với vị trí cân bằng O 1 cách vị trí lò xo không biến dạng O là:
![]()
![]()
Quãng đường đi được của m trong giai đoạn này (từ A 1 (biên ban đầu) đến A 2 (biên lúc sau)) là:
![]()
![]()
Thời gian chuyển động của m trong giai đoạn này là:
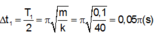
![]()
- Giai đoạn 2: Từ sau giai đoạn 1 đến lúc lò xo trở về trạng thái tự nhiên lần thứ 3. Lúc này hệ (m + M) dao động điều hòa quanh vị trí cân bằng O với biên độ và chu kì:
![]()
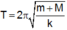
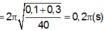
Khi lò xo trở về trạng thái tự nhiên lần thứ 3 cũng là thời điểm m đi qua O lần thứ 2. Khi đó m đã đi được quãng đường
![]() trong thời gian
trong thời gian ![]()
- Tốc độ trung bình chuyển động của m là:
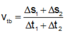
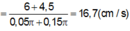

Đáp án B
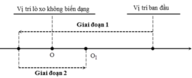
Nhận thấy rằng, lực ma sát trượt giữa M và m chỉ tồn tại khi dây D căng → tương ứng với chuyển động của m về phía bên trái. Do vậy ta có thể chia quá trình chuyển động của m thành các giai đoạn sau:
Giai đoạn 1: Dao động tắt dần quanh vị trí cân bằng tạm O 1
+ Tại vị trí cân bằng tạm, lực đàn hồi cân bằng với lực ma sát k Δ l 0 = μ M g → Δ l 0 = μ M g k = 0 , 2.0 , 3.10 40 = 1 , 5 c m
→ Biên độ dao động trong giai đoạn này là A1 = 4,5 – 1,5 = 3 cm.
+ Vật chuyển động đến biên thì đổi chiều lúc này lò xo bị nén một đoạn Δl = 3 – 1,5 = 1,5 cm.
Thời gian tương ứng trong giai đoạn này t 2 = T 2 2 = π m + M k = π 0 , 1 + 0 , 3 40 = 0 , 1 π s
Giai đoạn 2: m đổi chiều chuyển động → dây chùng không còn ma sát trượt nữa → hệ hai vật m + M dao động điều hòa quanh vị trí cân bằng O (vị trí lò xo không biến dạng)
+ Biên độ dao động của vật ở giai đoạn này A 2 = 1 , 5 c m (biên độ này nhỏ hơn A 2 m a x = μ g ω 2 2 = 2 cm để M không trượt trong quá trình dao động).
Thời gian tương ứng đến khi vật đổi chiều lần thứ hai t 1 = T 1 2 = π m k = π 0 , 1 40 = 0 , 05 π s
→ Tốc độ trung bình của m trong hai giai đoạn trên v t b = S t = 2 A 1 + 2 A 2 t 1 + t 2 = 2 3 + 1 , 5 0 , 05 π + 0 , 1 π = 19 , 1 c m / s

Đáp án D
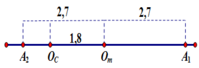
Ban đầu lò xo dãn đến vị trí A1. Khi m chuyển động về VTCB OC (vị trí lò xo tự nhiên) thì bị cản bởi lực ma sát nên VTCB bị lệch một đoạn .
![]()
Suy ra biên độ của m mới là A ' = 2 , 7 c m . m sẽ chuyển động đến A2 (lò xo nén cực đại).
Vật m bắt đầu quay về thì dây chùng nên m và M cùng dao động. Khi 2 vật cùng đến OC thì là lần 2 lò xo tự nhiên.
+ Tổng quãng đường đi được là
![]()
+ Từ A1 về A2 thì chỉ có m dao động, đi trong nửa chu kỳ
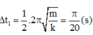
Từ A2 về OC thì 2 vật dao động, và từ biên về VTCB mất ¼ chu kỳ:
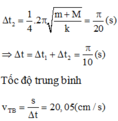

Đáp án B.
Chọn chiều dương như hình vẽ:
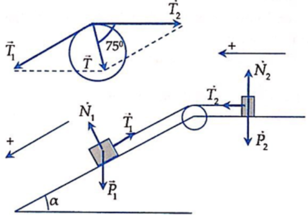
Áp dụng định luật II Niu-tơn cho mỗi vật :


Chọn A.
- Lực tác dụng lên mỗi vật như hình vẽ.

Do m2 > m1sinα nên m2 sẽ đi xuống.
- Áp dụng định luật II Niu-tơn cho mỗi vật:
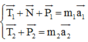
Do dây nhẹ, không dãn, ròng rọc không có khối lượng nên: T1 = T2 = T; a = a1 = a2.
- Chiếu các phương trình véctơ lên phương chuyển động của mỗi vật ta có:
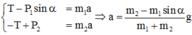

Đáp án B
+ Lực ma sát giữa M và m làm cho lò xo có độ dãn mới khác với VTCB:
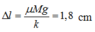
+ Lần 1 vật đổi chiều thì:
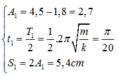
+ Lần 2 vật đổi chiều thì:
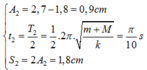
+ Lần thứ 3 vật đổi chiều thì:
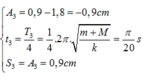
+ Tốc độ trung bình là:
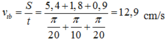
Chọn B