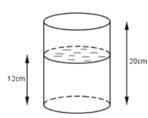
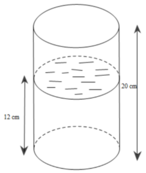
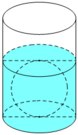
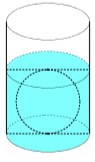
Một cái cốc hình trụ có bán kính đáy là 2cm, chiều cao 20cm. Trong cốc đang có một ít nước, khoảng cách giữa đáy cốc và mặt nước là 12cm (Hình vẽ). Một con quạ muốn uống được nước trong cốc thì mặt nước phải cách miệng cốc không quá 6cm. Con quạ thông minh mổ những viên đá hình cầu có bán kính 0,6cm thả vào cốc nước để mực nước dâng lên. Để uống được nước thì con quạ cần thả vào cốc ít nhất bao nhiêu viên bi?
A. 27
B. 30
C. 29
D. 28









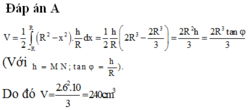




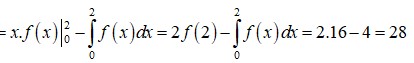
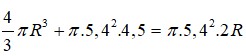
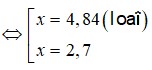
Đáp án D
Phương pháp:
+) Thể tích khối nước ít nhất cần dâng lên = Tổng thể tích đá thả vào.
+) Số viên đá = Tổng thể tích đá thả vào : Thể tích 1 viên đá