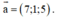Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Gọi H là hình chiếu vuông góc của điểm M trên đường thẳng Δ. Ta có:
H ∈ Δ => H(1 + t; 2 + t; 1 + 2t)
u Δ → = (1; 1; 2), MH → = (1- t; t + 1; 2t - 3)
MH ⊥ Δ <=> u Δ → . MH → = 0 <=> 1.(t - 1) + 1.(t + 1) + 2(2t - 3) = 0
<=> 6t - 6 = 0 <=> t = 1 => H(2; 3; 3)
Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)
Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: 
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: 
Đáp án B
Đường thẳng ∆ có vecto chỉ phương u → (2; -3; 2)
Đường thẳng d đi qua M(4;3;1) và song song với đường thẳng ∆ nên có vecto chỉ phương là u → (2; -3; 2). Phương trình chính tắc của đường thẳng d là:
Mặt phẳng (P) qua A và vuông góc d có phương trình:
\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow2x+2y+z-1=0\)
Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:
\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn:
\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng
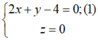
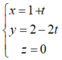
Chọn đáp án C.
nên một vectơ chỉ phương của đường phân giác của góc nhọn tạo bởi d và Δ là
Nhận thấy tọa độ điểm A thỏa mãn phương trình ở phương án C nên phương án đúng là C.
Cách 2: Đường thẳng d và đường thẳng Δ có vectơ chỉ phương lần lượt là
của đường phân giác của góc nhọn tạo bởi d và Δ thì
Kiểm tra từng phương án đến khi tìm được phương án đúng.
Tọa độ của điểm A không thỏa mãn phương trình ở phương án B nên loại phương án này.
- Phương án A: Đường thẳng có vectơ chỉ phương