Tìm giá trị của m để phương trình có nghiệm, rồi tính tổng và tích các nghiệm theo m.
x2 + 2(m – 1)x + m2 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 3 2017
a) Phương trình x 2 − 2 x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ ' = ( − 1 ) 2 − 1 ⋅ m = 1 − m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: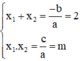 
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
b) Phương trình
x 2 + 2 ( m − 1 ) x + m 2 = 0 C ó ( a = 1 ; b = 2 ( m − 1 ) c = m 2 nên b ' = m − 1 ⇒ Δ ' = b ' 2 − a c = ( m − 1 ) 2 − m 2 = − 2 m + 1
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: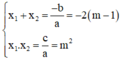 
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m 2
CM
2 tháng 11 2019
Phương trình x2 – 2x + m = 0
Có a = 1; b = -2; c = m nên b’= -1
⇒ Δ’ = (-1)2 – 1.m = 1 – m
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ 1 – m ≥ 0 ⇔ m ≤ 1.
Khi đó, theo định lý Vi-et: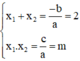 
Vậy với m ≤ 1, phương trình có hai nghiệm có tổng bằng 2; tích bằng m.
A
8 tháng 6 2023
a) Để phương trình có 2 nghiệm phân biệt
<=> \(\Delta=\left[-\left(4m+3\right)^2\right]-4.2.\left(2m-1\right)=16m^2+24m+9-16m+8=16m^2+8m+1+16=\left(4m+1\right)^2+16>0\)
với mọi giá trị của m.
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m.
b) Vì phương trình luôn có 2 nghiệm phân biệt với mọi giá trị của m nên ta có: x1+x2= \(\dfrac{4m+3}{2}\)và x1.x2=\(\dfrac{2m-1}{2}\)
CM
15 tháng 3 2018
2 x 2 – (4m + 3)x + 2 m 2 – 1 = 0 (2)
Phương trình (2) có nghiệm khi và chỉ khi ∆ ≥ 0
Ta có: ∆ = - 4 m + 3 2 – 4.2(2 m 2 – 1)
= 16 m 2 + 24m + 9 – 16 m 2 + 8 = 24m + 17
∆ ≥ 0 ⇔ 24m + 17 ≥ 0 ⇔ m ≥ -17/24
Vậy khi m ≥ -17/24 thì phương trình đã cho có nghiệm.
Giải phương trình (2) theo m:
CM
17 tháng 11 2018
Thay x = −3 vào phương trình
(m – 2)x2 – (m2 + 1)x + 3m = 0, ta có:
(m – 2) (−3)2 – (m2 + 1) (−3) + 3m = 0
⇔ 9m – 18 + 3m2 + 3 + 3m = 0
⇔ 3m2 + 12m – 15 = 0
⇔ m2 + 4m – 5 = 0
⇔ m2 – m + 5m – 5 = 0
⇔ m (m – 1) + 5 (m – 1) = 0
⇔ (m – 1) (m + 5) = 0 ⇔ m = 1 m = − 5
Suy ra tổng các giá trị của m là (−5) + 1 = −4
Đáp án cần chọn là: B
CM
16 tháng 1 2017
a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: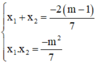 
Khi đó:
QD
4 tháng 4 2017
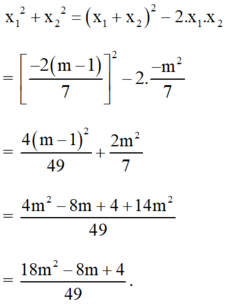
a) Phương trình x2– 2x + m = 0 có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó x1 + x2 = 2, x1 . x2 = m
b) Phương trình x2 – 2(m – 1)x + m2 = 0 có nghiệm khi
\(\text{∆}'=m^2-2m+1-m^2=1-2m\ge0\)' hay khi m \(\le\dfrac{1}{2}\)
Khi đó x1 + x2 = -2(m – 1), x1 . x2 = m2
4 tháng 4 2017
a) Phương trình x2– 2x + m = 0 có nghiệm khi ∆' = 1 - m ≥ 0 hay khi m ≤ 1
Khi đó x1 + x2 = 2, x1 . x2 = m
b) Phương trình x2 – 2(m – 1)x + m2 = 0 có nghiệm khi
∆' = m2 - 2m + 1 – m2 = 1 – 2m ≥ 0 hay khi m ≤
Khi đó x1 + x2 = -2(m – 1), x1 . x2 = m2
DT
23 tháng 4 2022
\(a.\Leftrightarrow mx^2+2mx-x+m+2=0\)
\(\Leftrightarrow mx\left(x+2\right)+\left(m+2\right)-x=0\)
\(\Leftrightarrow\left(m+2\right)\left(mx+1\right)-x=0\)
\(\Rightarrow\left\{{}\begin{matrix}m=\left(0+x\right):\left(mx+1\right)-2\\m=[\left(0+x\right):\left(m+2\right)-1]:x\end{matrix}\right.\)
Phương trình x2 + 2(m – 1)x + m2 = 0
Có a = 1; b = 2(m – 1); c = m2 nên b’ = m-1
⇒ Δ’ = b'2 – ac = (m – 1)2 – m2 = - 2m + 1.
Phương trình có nghiệm ⇔ Δ’ ≥ 0 ⇔ - 2m + 1 ≥ 0 ⇔ m ≤ 1/2.
Khi đó, theo định lý Vi-et: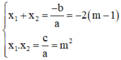
Vậy với m ≤ ½, phương trình có hai nghiệm có tổng bằng -2(m – 1), tích bằng m2