Giải phương trình 2 x 2 + 5 x = 0 bằng cách đặt nhân tử chung để đưa nó về phương trình tích.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(x - 2 ) + 3( x 2 – 2) = 0 ⇔ (x - 2 )+ 3(x + 2 )(x - 2 ) = 0
⇔ (x - 2 )[1 + 3(x + 2 )] = 0 ⇔ (x - 2 )(1 + 3x + 3 2 ) = 0
⇔ x - 2 = 0 hoặc 1 + 3x + 3 2 = 0
x - 2 = 0 ⇔ x = 2
1 + 3x + 3
2
= 0 ⇔ x = 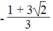
Vậy phương trình có nghiệm x =
2
hoặc x = 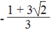

Tham khảo bài này :
(3x+1)(7x+3)=(5x-7)(3x+1)
<=> (3x+1)(7x+3)-(5x-7)(3x+1)=0
<=> (3x+1)(7x+3-5x+7)=0
<=> (3x+1)(2x+10)=0
<=> 2(3x+1)(x+5)=0
=> 3x+1=0 hoặc x+5=0
=> x= -1/3 hoặc x=-5
Vậy x = -1/3 hoặc x = -5
\(a,x^2+10x+25-4x\left(x+5\right)=0.\)
\(\Leftrightarrow\left(x+5\right)^2-4x\left(x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(5-3x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=0\\5-3x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-5\\x=\frac{5}{3}\end{cases}}}\)
\(b,\left(4x-5\right)^2-2\left(16x^2-25\right)=0\)
\(\Leftrightarrow\left(4x-5\right)^2-2\left(4x+5\right)\left(4x-5\right)=0\)
\(\Leftrightarrow-\left(4x-5\right)\left(4x+15\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}4x-5=0\\4x+15=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{5}{4}\\x=-\frac{15}{4}\end{cases}}}\)

Ta có: x 3 – 5 x 2 –x +5 = 0 ⇔ x 2 ( x -5) – ( x -5) =0
⇔ (x -5)(x2 -1) =0 ⇔ (x -5)(x -1)(x +1) =0
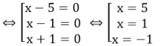
Vậy phương trình đã cho có 3 nghiệm :x1 = 5;x2 =1;x3=-1

(x2 + 2x – 5)2 = (x2 – x + 5)2
⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ [(x2 + 2x – 5) – (x2 – x + 5)].[(x2 + 2x – 5) + (x2 – x + 5)] = 0
⇔ (3x – 10)(2x2 + x ) = 0
⇔ (3x-10).x.(2x+1)=0
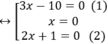
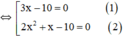
+ Giải (1): 3x – 10 = 0 ⇔ 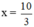
+ Giải (2):
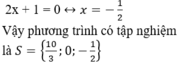

Ta có: x + 1 3 –x +1 = (x -1)(x -2)
⇔ x 3 +3 x 2 +3x +1 –x +1 = x 2 -2x –x +2
⇔ x 3 +2 x 2 +5x = 0 ⇔ x( x 2 + 2x + 5) =0
⇔ x =0 hoặc x 2 +2x +5 =0
Giải phương trình x 2 +2x +5 =0
∆ ’ = 1 2 - 1.5 = 1 - 5 = -4 < 0 ⇒ phương trình vô nghiệm
Vậy phương trình đã cho có 1 nghiệm : x=0

x 2 – 5 = (2x - 5 )(x + 5 )
⇔ (x + 5 )(x - 5 ) = (2x - 5 )(x + 5 )
⇔ (x + 5 )(x - 5 ) – (2x - 5 )(x + 5 ) = 0
⇔ (x + 5 )[(x - 5 ) – (2x - 5 )] = 0
⇔ (x + 5 )(- x) = 0 ⇔ x + 5 = 0 hoặc – x = 0
x + 5 = 0 ⇔ x = - 5
x = 0 ⇔ x = 0
Vậy phương trình có nghiệm x = - 5 hoặc x = 0.

Cách 1:
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 - 4(x2 – 2x + 1) = 0
⇔ (x + 1)2 - 22. (x -1)2 = 0
⇔ (x + 1)2 – [ 2(x – 1)]2 =0
⇔ [(x+ 1) + 2( x- 1)]. [(x+ 1) - 2( x- 1)]= 0
⇔ ( x+1+ 2x -2) . (x+1 – 2x + 2) =0
⇔ ( 3x- 1).( 3- x) = 0
⇔ 3x – 1 = 0 hoặc 3 – x= 0
+) 3x – 1 = 0 ⇔ 3x = 1 ⇔ x = 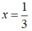
+) 3 – x = 0 ⇔ x= 3
Vậy tập nghiệm của phương trình đã cho là:
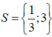
* Cách 2: Ta có:
(x + 1)2 = 4(x2 – 2x + 1)
⇔ (x + 1)2 - 4(x2 – 2x + 1) = 0
⇔ x2 + 2x +1- 4x2 + 8x – 4 = 0
⇔ - 3x2 + 10x – 3 = 0
⇔ (- 3x2 + 9x) + (x – 3) = 0
⇔ -3x (x – 3)+ ( x- 3) = 0
⇔ ( x- 3). ( - 3x + 1) = 0
⇔ x - 3 = 0 hoặc -3x + 1= 0
+) x - 3 = 0 x = 3
+) - 3x + 1 = 0 - 3x = - 1 ⇔ x = 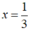
Vậy tập nghiệm của phương trình đã cho là:
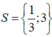
\(\left(x+1\right)^2=4\left(x^2-2x+1\right)\)
\(< =>\left(x+1\right)^2=\left(2x-2\right)^2\)
\(< =>\left(x+1-2x+2\right)\left(x+1+2x-2\right)=0\)
\(< =>\orbr{\begin{cases}-x+3=0\\3x-1=0\end{cases}}\)
\(< =>\orbr{\begin{cases}x=3\\x=\frac{1}{3}\end{cases}}\)
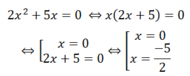
Vậy phương trình có hai nghiệm
x 1 = 0 ; x 2 = ( - 5 ) / 2