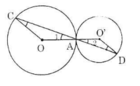
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.
Hình 89
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
3 tháng 6 2019
Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
suy ra C ^ = O A C ^ 1
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'
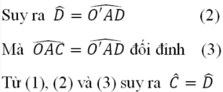
Vậy OC // O'D (có hai góc so le trong bằng nhau).
SG
1
KD
25 tháng 4 2017
Tam giác COA cân: ∠C = ∠A1
Tam giác DO’A cân: ∠D = ∠A2
Mà ∠A1 = ∠A2 (đối đỉnh)
⇒ ∠C = ∠D ⇒ OC//O’D
30 tháng 9 2021
Ta có \(\widehat{OAC}=\widehat{O'AD}\left(đối.đỉnh\right)\)
Mặt khác \(\Delta OAC.cân.tại.O\left(OA=OC\right)\)
Nên \(\widehat{OAC}=\widehat{OCA}\)
Tương tự \(\Delta O'AD.cân.tại.O'\left(O'A=O'D\right)\)
Nên \(\widehat{O'AD}=\widehat{O'DA}\)
\(\Rightarrow\widehat{OCA}=\widehat{ADO'}\)
Mà 2 góc này ở vị trí so le trong
Vậy \(OC//O'D\)
CM
7 tháng 5 2018
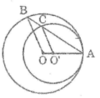
Ta có: OA = OB (= R)
Suy ra tam giác AOB cân tại O
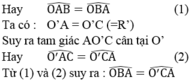
Suy ra: OB // O’C (vì có hai góc ở vị trí đồng vị bằng nhau)
3 tháng 5 2022
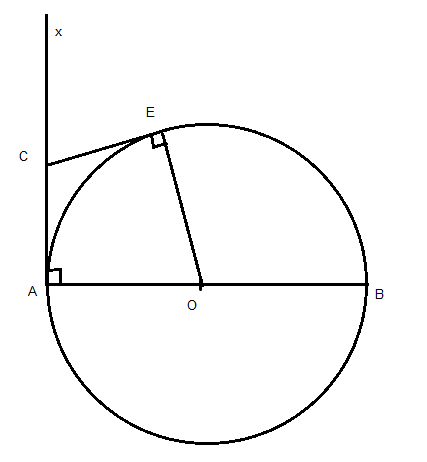
a) xét tứ giác ACEO có :
\(\widehat{CAO}\) = 900 ( tính chất tiếp tuyến )
\(\widehat{CEO}\) = 900 ( tính chất tiếp tuyến )
ta có : \(\widehat{CAO}\) + \(\widehat{CEO}\) = 1800
mà hai góc này nằm ở vị trí đối nhau
==> tứ giác ACEO nội tiếp
hay bốn điểm A C E O cùng thuộc một đường tròn
CM
23 tháng 2 2018
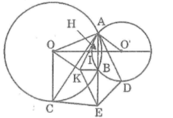
Vì AB ⊥ KB nên AE ⊥ KB
Lại có: AB = BE (tính chất đối xứng tâm)
Suy ra: KA = KE (tính chất đường trung trực) (3)
Ta có: IO = IO’ (gt)
IA = IK (chứng minh trên)
Tứ giác AOKO’ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: OK // O’A và OA // O’K
CA ⊥ O’A (vì CA là tiếp tuyến của đường tròn (O’))
OK // O’A (chứng minh trên)
Suy ra: OK ⊥ AC
Khi đó OK là đường trung trực của AC
Suy ra: KA = KC (tính chất đường trung trực) (4)
DA ⊥ OA (vì DA là tiếp tuyến của đường tròn (O))
O’K // OA (chứng minh trên)
Suy ra: O’K ⊥ DA
Khi đó O’K là đường trung trực của AD
Suy ra: KA = KD (tính chất đường trung trực) (5)
Từ (3), (4) và (5) suy ra: KA = KC = KE = KD
Vậy bốn điểm A, C, E, D cùng nằm trên một đường tròn.3
Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'
Vậy OC // O'D (có hai góc so le trong bằng nhau).