Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b =
π
4
...
Đọc tiếp
Tính giá trị biểu thức P = ( sina + sinb) 2+ ( cosa + cosb) 2 biết a - b = π 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 3 2018
a) √2 cos(x - π/4)
= √2.(cosx.cos π/4 + sinx.sin π/4)
= √2.(√2/2.cosx + √2/2.sinx)
= √2.√2/2.cosx + √2.√2/2.sinx
= cosx + sinx (đpcm)
b) √2.sin(x - π/4)
= √2.(sinx.cos π/4 - sin π/4.cosx )
= √2.(√2/2.sinx - √2/2.cosx )
= √2.√2/2.sinx - √2.√2/2.cosx
= sinx – cosx (đpcm).
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2020
\(A=cos^2a+cos^2b+2cosa.cosb+sin^2a+sin^2b+2sina.sinb\)
\(=cos^2a+sin^2a+cos^2b+sin^2b+2\left(cosa.cosb+sina.sinb\right)\)
\(=2+2cos\left(a-b\right)=2+2cos\frac{\pi}{3}=3\)
\(\left(cosa+sina\right)^2=\frac{36}{25}\Leftrightarrow1+2sina.cosa=\frac{36}{25}\)
\(\Rightarrow sin2a=\frac{36}{25}-1=\frac{11}{25}\)
\(cos2a=cos^2a-sin^2a=\left(cosa-sina\right)\left(cosa+sina\right)>0\)
\(\Rightarrow cos2a=\sqrt{1-sin^22a}=\frac{6\sqrt{14}}{25}\)
NH
0
PT
1
N5
1
LN
0
VN
2
NM
27 tháng 4 2021
TL:
sinA+sinB+sinC=1-cosA+cosB+cosC => Tam giác ABC Vuông tại A
NM
27 tháng 4 2021
Vế trái = sinA + sinB + sinC
= 2sin(A + B)/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2.cos(A - B)/2 + 2sinC/2.cosC/2
= 2cosC/2[cos(A - B)/2 + sinC/2]
=2.cosC/2.[cos(A - B)/2 + cos(A + B)/2]
= 4.cosC/2.cosB/2.cosA/2
Vế phải = 1 - cosA + cosB + cosC
= 2sin²A/2 + 2cos(B + C)/2.cos(B - C)/2
= 2.sinA/2[sinA/2 + cos(B - C)/2] (vì cos(B + C)/2 = sinA/2)
= 2.sinA/2[cos(B + C)/2 + cos(B - C)/2
= 4.sinA/2.cosB/2.cosC/2
Vậy sinA + sinB + sinC = 1 - cosA + cosB + cosC
<=> cosA/2.cosB/2.cosC/2 = sinA/2.cosB/2.cosC/2
<=> cosB/2.cosC/2(sinA/2 - cosA/2) = 0
mà cosB/2 ≠ 0 và cosC/2 ≠ 0
=> sinA/2 = cosA/2
<=> A/2 = 45o
<=> A = 90o
tam giác ABC vuông tại A
6 tháng 8 2019
Tự vẽ hình
Kẻ BH \(\perp\)AC và \(CK\perp\)AB
Tam giác AKC vuông tại K
=>CK=bsinA (1)
Tam giác BKC vuông tại K
=>CK=asinB (2)
Từ (1) (2)=>bsinA=asinB
<=>\(\frac{a}{sinA}=\frac{b}{sinB}\)
Chứng minh tương tự ta có :\(\frac{a}{sinA}=\frac{c}{sinC}\)
Vậy ....
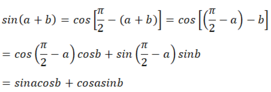
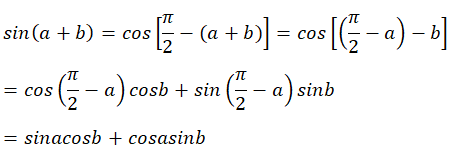
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)