Tính diện tích giới hạn bởi các đường cong y=(e+1)x; y = (ex + 1)x
A. e 5 - 19 100
B. 2 e 3 - 73 50
C. e 3 - 11 20
D. e 2 - 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
+) Xét phương trình: (x - 1)lnx = x - 1 ⇔ x = 1 hoặc x = e.
+ ) Diện tích cần tìm là:
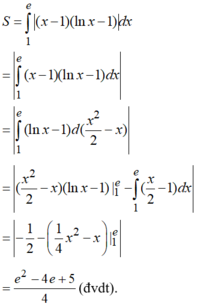

Chọn C.
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là:
(x – 1) ln(x + 1) = 0 <=> x = 1 hoặc x = 0
→ Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = (x – 1) ln(x = 1) và trục hoành là
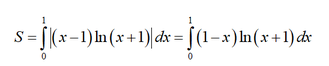
Đặt u = ln ( x + 1 ) d v = ( 1 - x ) d x ⇒ d u = 1 x + 1 d x v = 2 x - x 2 2
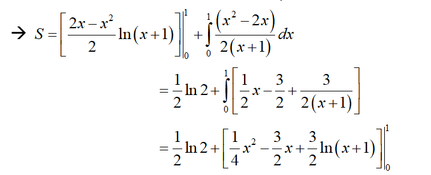
= 1 2 ln 2 - 5 4 + 3 2 ln 2 = - 5 4 + 2 ln 2
Chọn D.
Hoành độ giao điểm của hai đường là nghiệm của phương trình (e+1)x = ( 1 + e x ) x <=> x = 0 hoặc x =1
Diện tích cần tính là S = ∫ 0 1 x e x d x - ∫ 0 1 e x d x = ∫ 0 1 x d ( e x ) - e ∫ 0 1 x d x