Cho cấp số cộng u n có công sai d=-3 và u 2 2 + u 3 2 + u 4 2 đạt giá trị nhỏ nhất. Tính tổng S 100 của 100 số hạng đầu tiên của cấp số cộng đó.
A. -14 550
B. -14 400
C. -14 250
D. -15 450
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
18 tháng 8 2018
Đúng(0)
Những câu hỏi liên quan
CM
3 tháng 3 2018
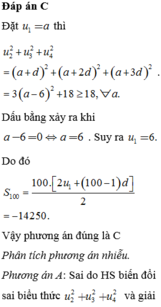
Chọn C
Sử dụng tính chất của cấp số cộng và công thức tính tổng n số hạng đầu của cấp số cộng là
S n = n . u 1 + n ( n - 1 ) 2 . d
CM
31 tháng 1 2018
Đáp án B
Ta có:
S = u 2 2 + u 3 2 + u 4 2 = u 1 − 3 2 + u 1 − 6 2 + u 1 − 9 2 = 3 u 1 2 − 36 u 1 + 126 .
Do đó S đạt GTNN khi u 1 = 6 .
Vậy S 100 = 100.6 + 100.99 2 . − 3 = − 14250 .
CM
5 tháng 10 2019
Chọn C.
Phương pháp : Sử dụng tính chất của cấp số cộng và công thức tính tổng n số hạng đầu của cấp số cộng là
AH
Akai Haruma
Giáo viên
9 tháng 11 2023
Lời giải:
Đặt $u_2=a$.
$u_2^2+u_3^2+u_4^2=a^2+(a-3)^2+(a-6)^2=3a^2-18a+45$
$=3(a-3)^2+18\geq 18$
Vậy $u_2^2+u_3^2+u_4^2$ đạt min =18 khi $a-3=0\Leftrightarrow a=3$
Tổng 100 số hạng đầu tiên:
$S_{100}=u_1+u_2+u_3+...+u_{100}$
$=(u_2-d)+u_2+(u_2+d)+(u_2+2d)+...+(u_2+98d)$
$=100u_2+(-1+0+1+2+...+98)d$
$=100.3+4850(-3)=-14250$
CM
7 tháng 4 2019
Chọn C.
Đặt a = u1 thì u22 + u32 + u42 = (a + d)2 + (a + 2d)2 + (a + 3d2 = 3a2 – 36a + 126 = 3(a – 6)2 + 18 ≥ 18 với mọi a.
Dấu bằng xảy ra khi a – 6 = 0 hay a = 6.
Suy ra 6 = u1.
Ta có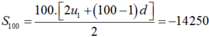 
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
\(u_2=u_1+d=-2+d\) ; \(v_2=v_1q=-2q\)
\(u_2=v_2\Rightarrow-2+d=-2q\Rightarrow d=2-2q\)
\(u_3=v_3+8\Leftrightarrow-2+2d=-2q^2+8\)
\(\Leftrightarrow-2+2\left(2-2q\right)=-2q^2+8\)
\(\Leftrightarrow2q^2-4q-6=0\Rightarrow\left[{}\begin{matrix}q=-1\Rightarrow d=4\\q=3\Rightarrow d=-4\end{matrix}\right.\)
CM
1 tháng 1 2017
Chọn A
Phương pháp:
Cấp số cộng ( u n ) có công sai d
u n = u 1 + ( n - 1 ) d
d = u n - u 1 n - 1
Cách giải:
u 3 2 + u 4 2 = ( u 1 + 2 d ) 2 + ( u 1 + 3 d ) 2
= ( u 1 - 8 ) 2 + ( u 1 - 12 ) 2
= 2 ( u 1 - 10 ) 2 + 8 ≥ 8
Vậy u 3 2 + u 4 2 đạt giá trị nhỏ nhất khi u 1 = 10
⇒ u 2019 = - 8062