Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
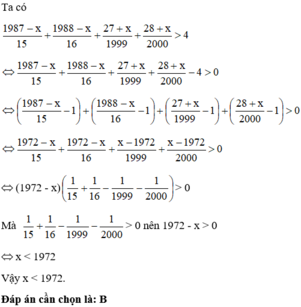
BPT \(\Leftrightarrow\dfrac{x+1987}{2002}+\dfrac{x+1988}{2003}-\dfrac{x+1989}{2004}+\dfrac{x+1990}{2005}>0\)
\(\Leftrightarrow\left(\dfrac{x+1987}{2002}-1\right)+\left(\dfrac{x+1988}{2003}-1\right)-\left(\dfrac{x+1989}{2004}-1\right)-\left(\dfrac{x+1990}{2005}-1\right)>0\)
\(\Leftrightarrow\dfrac{x-15}{2002}+\dfrac{x-15}{2003}-\dfrac{x-15}{2004}-\dfrac{x-15}{2005}>0\)
\(\Leftrightarrow\left(x-15\right)\left(\dfrac{1}{2002}+\dfrac{1}{2003}-\dfrac{1}{2004}-\dfrac{1}{2005}\right)>0\)
Vì \(\dfrac{1}{2002}+\dfrac{1}{2003}-\dfrac{1}{2004}-\dfrac{1}{2005}>0\)
\(\Rightarrow x-15>0\)
\(\Leftrightarrow x>15\)
Vậy bpt có nghiệm x > 15
\(\dfrac{x+1987}{2002}+\dfrac{x+1988}{2003}-2>\dfrac{x+1989}{2004}+\dfrac{x+1990}{2005}-2\)
\(\Leftrightarrow\left(\dfrac{x+1987}{2002}-1\right)+\left(\dfrac{x+1988}{2003}-1\right)\)
\(-\left(\dfrac{x+1989}{2004}-1\right)-\left(\dfrac{x+1990}{2005}-1\right)\)
quy đồng lên ta được:
\(\left(\dfrac{x+1987-2002}{2002}\right)+\left(\dfrac{x-1998-2003}{2003}\right)\)
\(-\left(\dfrac{x+1989-2004}{2004}\right)-\left(\dfrac{x+1990-2005}{2005}\right)>0\)
\(\Leftrightarrow\left(\dfrac{x-15}{2002}\right)+\left(\dfrac{x-15}{2003}\right)-\left(\dfrac{x-15}{2004}\right)-\left(\dfrac{x-15}{2005}\right)>0\)
đặt nhân tử chung ta được:
\(\Leftrightarrow\left(x-15\right)\left(\dfrac{1}{2002}+\dfrac{1}{2003}-\dfrac{1}{2004}-\dfrac{1}{2005}\right)>0\)
Vì:
\(\left(\dfrac{1}{2002}+\dfrac{1}{2003}-\dfrac{1}{2004}-\dfrac{1}{2005}\in Z\right)\) nên ta xét \(x-15>0\Rightarrow x>15\)
có thể đúng or có thể sai, các bn chọn ý nào?
thanks *-<
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
\(\dfrac{x-90}{10}+\dfrac{x-76}{12}+\dfrac{x-58}{14}+\dfrac{x-36}{16}+\dfrac{x-15}{17}=15\)
\(\Leftrightarrow\dfrac{x-90}{10}-1+\dfrac{x-76}{12}-2+\dfrac{x-58}{14}-3+\dfrac{x-36}{16}-4+\dfrac{x-15}{17}-5=0\)
\(\Leftrightarrow\dfrac{x-100}{10}+\dfrac{x-100}{12}+\dfrac{x-100}{14}+\dfrac{x-100}{16}+\dfrac{x-100}{17}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{10}+\dfrac{1}{12}+\dfrac{1}{14}+\dfrac{1}{16}+\dfrac{1}{17}\right)=0\)
\(\Leftrightarrow x-100=0\) (do \(\dfrac{1}{10}+\dfrac{1}{12}+\dfrac{1}{14}+\dfrac{1}{16}+\dfrac{1}{17}\ne0\))
\(\Leftrightarrow x=100\)
