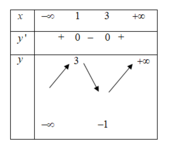
Cho hàm số y = a x 3 + bx 2 + c x + d có bảng biến thiên:
Cho các mệnh đề:
(1) Hệ số b < 0
(2) Hàm số có y CD = 2 ; y CT = - 2
(3) y''(0) < 0
(4) Hệ số c = 0, d = 1
Có bao nhiêu mệnh đề đúng:
A. 1
B. 2
C. 3
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: +) Khảo sát sự biến thiên của đồ thị hàm số.
+) Hàm số đạt cực trị tại điểm x = x 0 ⇔ y ' x 0 = 0 và x = x 0 được gọi là điểm cực trị.
+) Hàm số đạt cực trị tại điểm x = x 0 thì y x 0 là giá trị cực trị.


Như vậy có 3 mệnh đề đúng.
Chú ý: Học sinh thường giá trị cực trị và
điểm cực trị nên có thể chọn sai mệnh dề (2) đúng.

Đáp án A
Phương pháp: Dựa vào BBT để kết luận tính đơn điệu của hàm số và suy ra các giá trị a, c tương ứng.
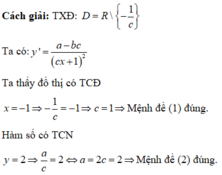
Theo BBT ta thấy hàm số đồng biến trên từng khoảng xác định của hàm số.
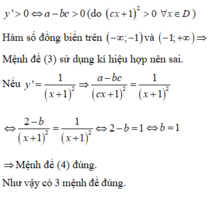

\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)

Đáp án D
Khẳng định số II sai.
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng - ∞ ; - 2

Đáp án D
Khẳng định số II sai. Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( − ∞ ; − 2 )
Đáp án đúng : C