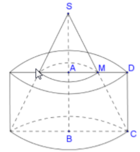
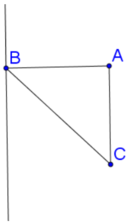
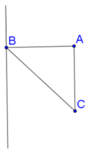
Cho tam giác vuông có hai cạnh góc vuông là a và b. Quay tam giác đó (cùng với phần trong của nó) quanh đường thẳng chứa cạnh huyển, ta được một khối tròn xoay có thể tích bằng
A. π a 2 b 2 3 a 2 + b 2
B. π 3 b 2 a 2 + b 2
C. π a 2 b 2 3 a + b
D. π 3 a b a 2 + b 2

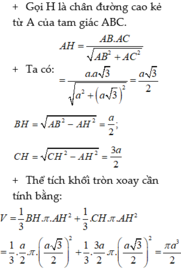
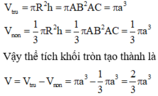
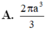
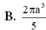
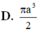
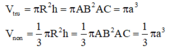
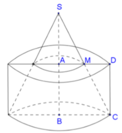
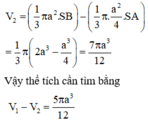
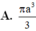
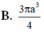

Đáp án A
Công thức thể tích khối nón V n o n = 1 3 π R 2 h ;
Ở đây R = O C .
Ta có 1 O C 2 = 1 C A 2 + 1 C B 2 = 1 a 2 + 1 b 2 = a 2 + b 2 a 2 b 2 ⇒ O C = a b a 2 + b 2 = R
Thể tích khối tròn xoay cần tính
V = 1 3 π O C 2 . O B + 1 3 π O C 2 . O A = 1 3 π R 2 . A B = 1 3 π a 2 b 2 a 2 + b 2 . a 2 + b 2 = π 3 . a 2 b 2 a 2 + b 2