Thể tích của khối tứ diện OABC có O A = O B = O C = a và O A , O B , O C đôi một tạo với nhau một góc 60 ° bằng
A. a 3 6
B. a 3 3
C. 2 a 3 12
D. 2 a 3 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D

Từ giả thiết suy ra: ΔABC cân tại A có:

Gọi I là trung điểm của BC ⇒ A I ⊥ B C
Giả sử H là trực tâm của tam giác ABC.
Ta thấy O A ⊥ O B C
Vì O B ⊥ O A C ⇒ O B ⊥ A C và A C ⊥ B H nên A C ⊥ O B H ⇒ O H ⊥ A C ( 1 )
B C ⊥ O A I ⇒ O H ⊥ B C ( 2 )
Từ (1) và (2) suy ra O H ⊥ A B C
Có O I = 1 2 B C = a 2 2 = O A
=> ΔAOI vuông cân tại O => H là trung điểm AI và O H = 1 2 A I = a 2
Khi đó:


Đáp án D
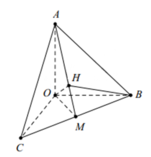
Gọi M là trung điểm của B C ⇒ B M ⊥ O A M
Vì O H ⊥ A B C ⇒ 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ O H = a 2
Tam giác OAH vuông tại H, có A H = O A 2 − O H 2 = a 2
Diện tích tam giác vuông OAH là S Δ O A H = 1 2 . O H . A H = a 2 8
Thể tích khối chóp OABH là
V O A B H = 1 3 . B M . S Δ O A H = 1 3 . a 2 2 . a 2 8 = a 3 2 48

Đáp án D
Ta có: V O . A B C = 1 6 O A . O B . O C = 6 ⇒ O C = 3
Lại có 1 d O ; A B C 2 = 1 O A 2 + 1 O B 2 + 1 O C 2 ⇒ d O ; A B C = 12 41
Đáp án đúng : C