Cho phương trình : mx2 - 2x - 4m - 1 = 0
a. Chứng mình rằng với mọi giá trị của m ≠ 0 phương trình đã cho có hai nghiệm phân biệt.
b. Tìm giá trị của m để -1 là một nghiệm của phương trình. Sau đó tìm nghiệm còn lại.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
31 tháng 5 2021
\(x^{2^{ }}+2\left(m-1\right)x-6m-7=0\left(1\right)\)
a) \(Dental=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-6m-7\right)\)
\(< =>4\cdot\left(m^2-2m+1\right)+24m+28\)
\(< =>4m^2-8m+4+24m+28\)
\(< =>4m^2+16m+32\)
\(< =>\left(2m+4\right)^2+16>0\) với mọi m
Vậy phương (1) luôn có 2 nghiệm phân biệt với mọi m
b) Theo định lí vi ét ta có:
x1+x2= \(\dfrac{-2\left(m-1\right)}{1}=-2m+1\)
x1x2= \(-6m-7\)
NP
22 tháng 4 2023
quy đồng
khử mẫu
tách sao cho có tích và tổng
thay x1x2 x1+x2
kết luận
mặt xấu vl . . .
7 tháng 5 2021
a) Đây là phương trình bậc 2 ẩn x có
Δ = (-m)2 - 4(m-1)
= m2-4m+4 = (m-2)2
Do (m-2)2≥0 ∀m => Δ≥0 ∀m
Vậy phương trình luôn có nghiệm với mọi m.
b) Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=m\left(1\right)\\x_1x_2=m-1\left(2\right)\end{matrix}\right.\)
\(x_1=2x_2\left(3\right)\)
Từ (1)(3) ta có hệ phương trình: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1=2x_2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}3x_2=m\\x_1=2x_2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}x_2=\dfrac{m}{3}\\x_1=\dfrac{2m}{3}\end{matrix}\right.\)
Thay \(x_1=\dfrac{2m}{3};x_2=\dfrac{m}{3}\) vào (2) ta có:
\(\dfrac{2m}{3}.\dfrac{m}{3}=m-1\)
<=> 2m2 = 9(m - 1)
<=> 2m2 - 9m + 9 = 0
<=> (m - 3)(2m - 3) = 0
<=> \(\left[{}\begin{matrix}m-3=0\\2m-3=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}m=3\\m=\dfrac{3}{2}\end{matrix}\right.\)
Vậy tại m ∈\(\left\{3;\dfrac{3}{2}\right\}\) thì hai nghiệm của phương trình thoả mãn x1=2x2
KV
7 tháng 5 2021
a) Ta có:
\(\Delta=b^2-4ac=\left(-m\right)^2-4.1.\left(m-1\right)\)
\(=m^2-4m+4=\left(m-2\right)^2\ge0\) với mọi m
Vậy phương trình đã cho luôn có nghiệm với mọi m
b) Do phương trình luôn có nghiệm với mọi m
Theo định lý Vi-ét, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left(-m\right)}{1}=m\left(1\right)\\x_1x_2=\dfrac{c}{a}=\dfrac{m-1}{1}=m-1\left(2\right)\end{matrix}\right.\)
Mà \(x_1=2x_2\), thay vào (1) ta có:
\(2x_2+x_2=3\Leftrightarrow3x_2=m\Leftrightarrow x_2=\dfrac{m}{3}\)
\(\Rightarrow x_1=2x_2=\dfrac{2m}{3}\)
Thay \(x_1=\dfrac{2m}{3};x_2=\dfrac{m}{3}\) vào (2) ta có:
\(\dfrac{2m}{3}.\dfrac{m}{3}=m-1\)
\(\Leftrightarrow2m^2=9m-9\)
\(\Leftrightarrow2m^2-9m+9=0\) (*)
\(\Delta_m=\left(-9\right)^2-4.2.9=9\)
Phương trình (*) có 2 nghiệm:
\(m_1=\dfrac{-\left(-9\right)+\sqrt{9}}{2.2}=3\)
\(m_2=\dfrac{-\left(-9\right)-\sqrt{9}}{2.2}=\dfrac{3}{2}\)
Vậy \(m=3;m=\dfrac{3}{2}\) thì phương trình đã cho có hai nghiệm \(x_1;x_2\) thỏa mãn \(x_1=2x_2\)
TN
9 tháng 5 2015
a, Với m=2 thì phương trình (1) trở thành
x mũ 2 + 2(2+2)x +4.2 -1 =0
<=> x mũ 2 + 8x +7 =0
<=> x mũ 2 + x + 7x +7 =0
<=> (x+1)(x+7) =0
<=> x= -1 hoặc x= -7
b, Ta có:
penta' = (m+2)mũ2 - 4m -1
= m m 2 +4m +4 -4m -1
= m mũ2 +3
vì m mũ2 luôn > hoặc = 0 với mọi m
suy ra m mũ2 +3 luôn >0 với mọi m
suy ra penta' >0 hay có hai nghiệm phân biệt (đpcm)
CÒN PHẦN SAU THÌ MK KO BIẾT LÀM .... THÔNG CẢM
27 tháng 1 2022
a/ Xét pt :
\(x^2-2\left(m-1\right)+2m-5=0\)
\(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-2m+1-2m+5=m^2-4m+6=\left(m-2\right)^2+2>0\forall m\)
\(\Leftrightarrow\) pt luôn có 2 nghiệm pb với mọi m
b/ Phương trình cớ 2 nghiệm trái dấu
\(\Leftrightarrow2m-5< 0\)
\(\Leftrightarrow m< \dfrac{5}{2}\)
c/ Theo định lí Vi - et ta có :
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1.x_2=2m-5\end{matrix}\right.\)
\(A=x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1.x_2\)
\(=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-8m+4-4m+10\)
\(=4m^2-12m+14=4\left(m^2-3m+\dfrac{9}{4}\right)+5=4\left(m-\dfrac{3}{2}\right)^2+5\ge5\)
\(A_{min}=5\Leftrightarrow m=\dfrac{3}{2}\)
27 tháng 1 2022
1, \(\Delta'=\left(m-1\right)^2-\left(2m-5\right)=m^2-4m+6=\left(m-2\right)^2+2>0\)
Vậy pt luôn có 2 nghiệm pb với mọi m
2, Vì pt có 2 nghiệm trái dấu
\(x_1x_2=\dfrac{c}{a}=2m-5< 0\Leftrightarrow m< \dfrac{5}{2}\)
3, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=2m-5\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2-2x_1x_2=4\left(m-1\right)^2-2\left(2m-5\right)\)
\(=4m^2-12m+14=4m^2-2.2m.3+9+6\)
\(=\left(2m-3\right)^2+6\ge6\forall m\)
Dấu ''='' xảy ra khi m = 3/2
Vậy với m = 3/2 thì A đạt GTNN tại 6
10 tháng 4 2021
a, Thay m = -1 vào phương trình trên ta được
\(x^2+4x-5=0\)
Ta có : \(\Delta=16+20=36\)
\(x_1=\frac{-4-6}{2}=-5;x_2=\frac{-4+6}{2}=1\)
Vậy với m = -1 thì x = -5 ; x = 1
b, Vì x = 2 là nghiệm của phương trình trên nên thay x = 2 vào phương trình trên ta được :
\(4+8+3m-2=0\Leftrightarrow3m=-10\Leftrightarrow m=-\frac{10}{3}\)
Vậy với x = 2 thì m = -10/3
c, Để phương trình có 2 nghiệm phân biệt thì \(\Delta>0\)hay
\(16-4\left(3m-2\right)=16-12m+8=4m+8>0\)
\(\Leftrightarrow8>-4m\Leftrightarrow m>-2\)
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=-4\\x_1x_2=\frac{c}{a}=3m-2\end{cases}}\)
\(\Leftrightarrow x_1+x_2=-4\Leftrightarrow x_1=-4-x_2\)(1)
suy ra : \(-4-x_2+2x_2=1\Leftrightarrow-4+x_2=1\Leftrightarrow x_2=5\)
Thay vào (1) ta được : \(x_1=-4-5=-9\)
Mà \(x_1x_2=3m-2\Rightarrow3m-2=-45\Leftrightarrow3m=-43\Leftrightarrow m=-\frac{43}{3}\)
HP
6 tháng 6 2021
a, Khi m=2, phương trình trở thành:
\(2x^2-5x+2=0\)
\(\Leftrightarrow\left(2x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\)
Vậy với m=2, phương trình có nghiệm \(x=\dfrac{1}{2};x=2\)
b, \(\Delta=\left(m+3\right)^2-8m=m^2-2m+9=\left(m-1\right)^2+8>0,\forall m\)
\(\Rightarrow\) Phương trình đã cho có nghiệm với mọi m
Theo định lí Vi-et: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+3}{2}\\x_1x_2=\dfrac{m}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1^2+x_2^2+2x_1x_2=\dfrac{m^2+6m+9}{4}\\4x_1x_2=2m\end{matrix}\right.\)
\(\Rightarrow\left(x_1-x_2\right)^2=\dfrac{m^2-2m+9}{4}\)
\(\Rightarrow A=\left|x_1-x_2\right|=\dfrac{\sqrt{m^2-2m+9}}{2}=\dfrac{\sqrt{\left(m-1\right)^2+8}}{2}\ge\sqrt{2}\)
\(\Rightarrow minA=\sqrt{2}\Leftrightarrow m=1\)
6 tháng 6 2021
pt: \(2x^2-\left(m+3\right)x+m=0\left(1\right)\)
a, khi m=2 ta có: \(2x^2-5x+2=0\)(2)
\(\Delta=\left(-5\right)^2-4.2.2=9>0\)
vậy pt(2) có 2 nghiệm phan biệt \(x3=\dfrac{5+\sqrt{9}}{2.2}=2\)
\(x4=\dfrac{5-\sqrt{9}}{2.2}=0,5\)
b,từ pt(1) có \(\Delta=\left[-\left(m+3\right)\right]^2-4m.2=m^2+6m+9-8m\)
\(=m^2-2m+9=\left(m-1\right)^2+8>0\left(\forall m\right)\)
vậy \(\forall m\) pt(1) luôn có 2 nghiệm phân biệt x1,x2
điều kiện để pt(1) có 2 nghiệm phân biệt không âm khi
\(\left\{{}\begin{matrix}\Delta>0\\S>0\\P>0\end{matrix}\right.< =>\left\{{}\begin{matrix}\Delta>0\left(cmt\right)\\x1+x2>0\\x1.x2>0\end{matrix}\right.< =>\left\{{}\begin{matrix}\dfrac{m+3}{2}>0\\\dfrac{m}{2} >0\end{matrix}\right.\)\(< =>\left\{{}\begin{matrix}m>-3\\m>0\end{matrix}\right.\)
\(< =>m>0\)
theo vi ét =>\(\left\{{}\begin{matrix}x1+x2=\dfrac{m+3}{2}\\x1.x2=\dfrac{m}{2}\end{matrix}\right.\)
\(=>A=\left|x1-x2\right|\)
\(=>A=\sqrt{\left(x1-x2\right)^2}=\sqrt{\left(x1+x2\right)^2-4x1x2}\)
\(A=\sqrt{\left(\dfrac{m+3}{2}\right)^2-4\dfrac{m}{2}}=\sqrt{\dfrac{m^2+6m+9-8m}{4}}\)
\(A=\sqrt{\dfrac{\left(m-1\right)^2+8}{4}}=\dfrac{1}{2}\sqrt{\left(m-1\right)^2+8}\)\(\ge\sqrt{2}\)=>Min A=\(\sqrt{2}\)
dấu = xảy ra <=>m=1(TM)
a) mx2 – 2x – 4m – 1 = 0 (1)
Với m ≠ 0, ta có:
Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1
=
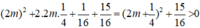với mọi m.
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.
b) x = -1 là nghiệm của phương trình (1)
⇔ m.(-1)2 – 2.(-1) – 4m – 1 = 0
⇔ m + 2 - 4m = 0
⇔ -3m + 1 = 0
⇔ m = 1/3.
Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.
Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))
⇒ x2 = 2/m + 1= 6 + 1 = 7.
Vậy nghiệm còn lại của (1) là 7.