Cho elip có phương trình: x 2 4 + y 2 1 = 1 Khi đó tọa độ hai đỉnh trên trục lớn của elip là.
A. A1( -1; 0) và A2( 1;0)
B. A1( 0; -1) và A2( 0; 1)
C. A1( 2;0) và A2( 1; 0)
D. A1( (-2;0) và A2(2;0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: b2= 4 mà b> 0 nên b= 2
- Hai đỉnh trên trục nhỏ là: B1( -2; 0) và B2( 2;0)
Chọn A

a) (E): 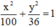 có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
có a = 10; b = 6 ⇒ c2 = a2 – b2 = 64 ⇒ c = 8.
+ Tọa độ các đỉnh của elip là: A1(-10; 0); A2(10; 0); B1(0; -6); B2(0; 6)
+ Tọa độ hai tiêu điểm của elip: F1(-8; 0) và F2(8; 0)
+ Vẽ elip:
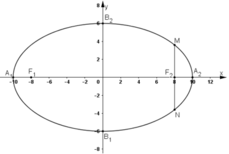
b) Ta có: M ∈ (E) ⇒ MF1 + MF2 = 2a = 20 (1)
MN // Oy ⇒ MN ⊥ F1F2 ⇒ MF12 – MF22 = F1F22 = (2c)2 = 162
⇒ (MF1 + MF2).(MF1 – MF2) = 162
⇒ MF1 – MF2 = 12,8 (Vì MF1 + MF2 = 20) (2).
Từ (1) và (2) ta có hệ phương trình
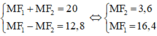
Vậy MN = 2.MF2 = 7,2.

a) 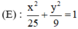 có a = 5, b = 3 ⇒ c = √(a2 – b2) = 4.
có a = 5, b = 3 ⇒ c = √(a2 – b2) = 4.
Tọa độ các đỉnh là A1 = (–5 ; 0) ; A2 = (5 ; 0) ; B1 = (0 ; –3) ; B2 = (0 ; 3)
Tọa độ hai tiêu điểm là F1 = (–4 ; 0) và F2 = (4 ; 0)
Độ dài trục lớn bằng A1A2 = 10
Độ dài trục nhỏ bằng B1B2 = 6.

a) Phương trình \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 10,b = 6 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{{10}^2} - {6^2}} = 8 \)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 8;0} \right),{F_2}\left( {8;0} \right)\)
Tọa độ các đỉnh: \(A(0;6),B(10;0),C(0; - 6),D( - 10;0)\)
Độ dài trục lớn 20
Độ dài trục nhỏ 12
b) Phương trình \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 5,b = 4 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{5^2} - {4^2}} = 3\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 3;0} \right),{F_2}\left( {3;0} \right)\)
Tọa độ các đỉnh: \(A(0;4),B(5;0),C(0; - 4),D( - 5;0)\)
Độ dài trục lớn 10
Độ dài trục nhỏ 8
c) \({x^2} + 16{y^2} = 16 \Leftrightarrow \frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{1} = 1\)
Vậy ta có phương trình chính tắc của elip đã cho là \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{1} = 1\)
Suy ra \(a = 4,b = 1 \Rightarrow c = \sqrt {{a^2} - {b^2}} = \sqrt {{4^2} - {1^2}} = \sqrt {15} \)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - \sqrt {15} ;0} \right),{F_2}\left( {\sqrt {15} ;0} \right)\)
Tọa độ các đỉnh: \(A(0;1),B(4;0),C(0; - 1),D( - 4;0)\)
Độ dài trục lớn 8
Độ dài trục nhỏ 2

Phương trình chính tắc của elip có dạng : E x 2 a 2 + y 2 b 2 = 1 ( a , b > 0 )
Ta có :
+ Độ dài trục lớn là 12 nên 2a= 12 => a= 6 .
+ Độ dài trục bé là 6 nên 2b = 6 => b= 3
Vậy phương trình của Elip là: x 2 36 + y 2 9 = 1 .
Chọn C.

Chọn C.
Phương trình chính tắc của elip có dạng (E):
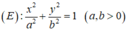
Ta có a = 6, b = 3, vậy phương trình của Elip là:
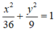

Chọn A.
Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇔ a = 5, a 2 = 25
Độ dài tiêu cự bằng 6 ⇒ 2c = 6 ⇔ c = 3
Ta có: a 2 - b 2 = c 2 ⇒ b 2 = a 2 - c 2 = 5 2 - 3 2 = 16
Vậy phương trình của elip (E) là:
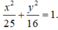
Ta có: a2= 4 mà a> 0 nên a= 2
- Hai đỉnh trên trục lớn là: . A1( (-2;0) và A2(2;0)
Chọn D