Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh đều bằng a. Tính theo a khoảng cách giữa hai đường thẳng AB và SC
A. a 6 2
B. a 3 3
C. a 6 3
D. a 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

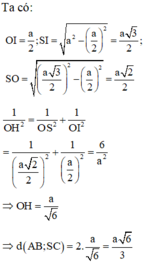

Đáp án C
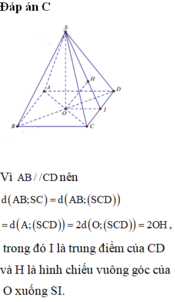
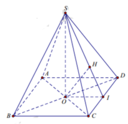
Vì A B / / C D nên d A B ; S C = d A B ; S C D
= d A ; S C D = 2 d O ; S C D = 2 O H , trong đó I là trung điểm của CD và H là hình chiếu vuông góc của O xuống SI.
Ta có: O I = a 2 ; S I = a 2 − a 2 2 = a 3 2 ; S O = a 3 2 2 − a 2 2 = a 2 2
1 O H 2 = 1 O S 2 + 1 O I 2 = 1 a 2 2 2 + 1 a 2 2 = 6 a 2 ⇒ O H = a 6
⇒ d A B ; S C = 2. a 6 = a 6 3

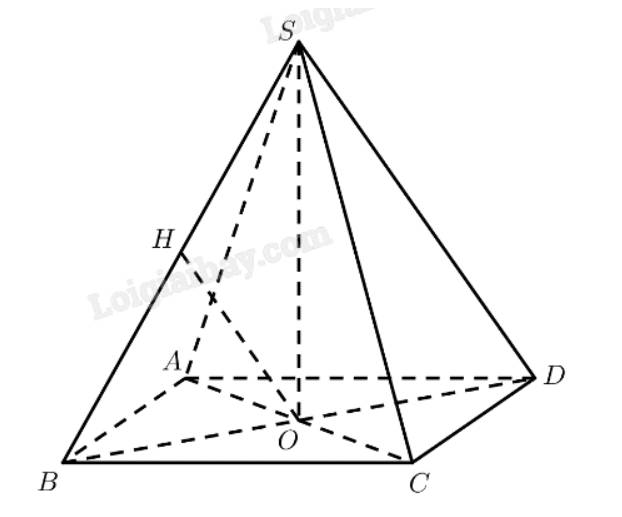
a) Kẻ \(OH \bot SB\left( {H \in SB} \right)\)
\(S.ABC{\rm{D}}\) là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AC\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\( \Rightarrow AC \bot \left( {SB{\rm{D}}} \right) \Rightarrow AC \bot OH\)
Mà \(OH \bot SB\)
\( \Rightarrow d\left( {AC,SB} \right) = OH\)
\(B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 \Rightarrow BO = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SBO\) vuông cân tại \(O\) có đường cao \(OH\)
\( \Rightarrow d\left( {AC,SB} \right) = OH = \frac{1}{2}SB = \frac{a}{2}\)
b) \({S_{ABC{\rm{D}}}} = A{B^2} = {a^2}\)
\({V_{S.ABC{\rm{D}}}} = \frac{1}{3}{S_{ABC{\rm{D}}}}.SO = \frac{{{a^3}\sqrt 2 }}{6}\)

Đáp án C
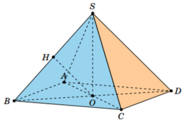
Gọi O là giao điểm của AC và BD. Ta có AC vuông góc với mặt phẳng (SBD) tại O. Kẻ OH vuông góc với SB, thì OH là khoảng cách cần tìm. Tam giác SOB vuông cân tại O, nên O H = S B 2 = a 2 .

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow\widehat{SCO}\) là góc giữa SC và (ABCD) hay \(\widehat{SCA}\) là góc giữa SC và (ABCD) (do A,C,O thẳng hàng)
\(AC=AB\sqrt{2}=a\sqrt{2}\)
\(\Leftrightarrow SA^2+SC^2=AC^2\Rightarrow\Delta SAC\) vuông cân tại S
\(\Rightarrow\widehat{SCA=45^0}\)

Đáp án D.
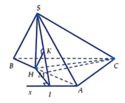
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
![]()
![]()
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
![]()
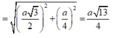
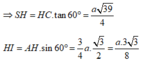
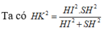
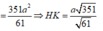
![]()
![]()