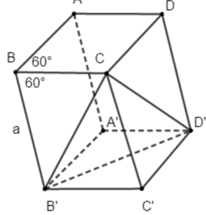
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc tại đỉnh B đều bằng 60 o .
Đường thẳng B’C vuông góc với đường thẳng:
A. AC
B. CD
C. BD
D. A’A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương án A, B và D đều sai
Phương án C đúng vì tam giác CB’D’ có ba cạnh bằng a, a√3,a√3 nên không thể vuông tại B’
Đáp án C

Đáp án A
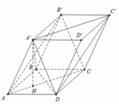
Do các góc phẳng đỉnh A đều bằng 60 ∘ và
nên các tam giác A ’ A D ; A ’ A B ; A B D là các tam giác đều cạnh 1.
Ta có:
A ' C ' / / A C ⇒ d A B ' ; A ' C ' = d A B ' C ; A ' C ' = d C ' ; A B ' C = 3 V C ' . A B ' C S . A B ' C
Mặt khác A ’ . A B D là hình tứ diện đều cạnh 1.
Ta có A H = 2 3 . A O = 3 3 ⇒ A ' H = A A ' 2 − A H 2 = 6 3 .
V = S A B C D = V A . C C ' B ' = 1 2 V A . C C ' B ' B = V 6 = 2 12
Δ A B ' C ' cân tại A có A B ' = A C = 3 ; B ' C = A ' D = 1
S A B ' C = 11 4 ⇒ d = 3. 2 12 11 4 = 22 11 .

Đáp án A
Theo giả thết ta có: ∆ A A ' B ⊥ ⇒ A B ⊥ A ' B ∆ A ' C D ⊥ ⇒ C D ⊥ A ' D ⇒ A B ⊥ A ' D ⇒ A B ⊥ ( A ' B D ) ⇒ A B ⊥ B D ⇒ B D = A D 2 - A B 2 = 5 a 2 - a 2 = 2 a ⇒ S A B C D = 2 S A B D = A B . A D = a . 2 a = 2 a 2
Kẻ đường cao AH trong ∆ A'BD , góc giữa AB' và (ABCD) là góc A'BH= 45 °
Do B'C // A'D nên góc giữa B'C và (ABCD) là góc A'DH= 45 ° ⇒ ∆ A ' B D vuông cân ⇒ A ' H = B D 2 = 2 a 2 = a từ đây tính được V A B C D . A ' B ' C ' D ' = A ' H . S A B C D = a . 2 a 2 = 2 a 3
Phương án A sai vì tam giác ACB’ có ba cạnh bằng a
Phương án C sai vì tam giác CB’D’ có ba cạnh a, a√3,a√3 nên không thể vuông tại B’
Phương án D sai vì góc giữa đường thẳng B’C và AA’ bằng 0 o
Phương án B đúng vì:
Đáp án B