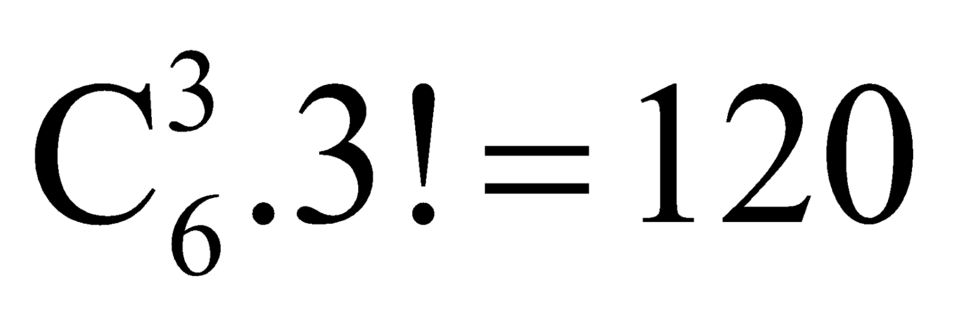Từ các chữ số 1,2,3,4 ta có thể tạo thành bao nhiêu số tự nhiên gồm 6 chữ số, trong đó chữ số 1 xuất hiện đúng 3lần, ba chữ số 2,3,4 hiện diện đúng 1 lần.
A. 120
B. 24
C. 360
D. 384
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Thêm vào hai chữ số 1 vào tập hợp các chữ số đã cho ta được tập E = {1,1,1,2,3,4}
Xem các số 1 là khác nhau thì mỗi hoán vị của 6 phần tử của E cho ta một số có 6 chữ số thỏa mãn bài toán. Như vậy ta có 6! số. Tuy nhiên khi hoán vị vủa ba số 1 cho nhau thì giá trị con số không thay đổi nên mỗi số như vậy ta đếm chúng đến 3! lần.
Vậy số các số thỏa mãn yêu cầu bài toán là 6 ! 3 ! = 4 . 5 . 6 = 120 s ố .
Chú ý: Ta có thể giải như sau, ta gọi số 6 chữ số cần tìm là a b c d e f , chọn 3 vị trí trong 6 vị trí để đặt ba chữ số 1 có C 6 3 cách, xếp 3 chữ số 2, 3, 4 vào ba vị trí còn lại có 3! cách do đó C 6 3 . 3 ! = 120

Số số thỏa mãn: \(\dfrac{9!}{5!}=3024\) số
(Đây là loại hoán vị lặp)

Số tự nhiên có 8 chữ số \(\overline{abcdefgh}\).
TH1: \(h=0\)
\(\overline{abcdefg}\) có \(\dfrac{7!}{2!.3!}=420\) cách lập.
\(\Rightarrow\) Lập được 420 số thỏa mãn yêu cầu.
TH2: \(h=5\)
\(\overline{abcdefg}\) có \(\dfrac{7!}{2!.3!}-\dfrac{6!}{2!.3!}=360\) cách lập.
\(\Rightarrow\) Lập được 360 số thỏa mãn yêu cầu.
Vậy lập được \(420+360=780\) số tự nhiên thỏa mãn yêu cầu bài toán.
Bạn có thể giải thích phần công thức được không vậy. Mình hiểu hơi chậm. Bạn thông cảm. Mình cảm ơn nhiều.

Xét các số tự nhiên có bảy chữ số được lập từ {1;2;2;2;3;4;5;6;7}.
Ta thấy có ![]() số như vậy.
số như vậy.
Tuy nhiên khi hoán vị vị trí của ba số 2 cho nhau thì số thu được không thay đổi.
Vậy có ![]() số thỏa yêu cầu bài toán.
số thỏa yêu cầu bài toán.
chọn B.

Chữ số 2 xuất hiện 3 lần.
Coi chữ số đc lập nên từ 6 chữ số tập \(A=\left\{1,2,2,2,3,4\right\}\)
Gọi số cần lập là \(\overline{abcdef}\in A\)
Chọn a có 6 cách chọn.
Xếp 5 số của \(A\backslash\left\{a\right\}\) vào 5 vị trí còn lại có 5! cách xếp.
Mà chữ số 2 lặp lại 3 lần\(\Rightarrow\) có 3! cách xếp.
Vậy số các số cần lập:
\(\dfrac{6\cdot5!}{3!}=120\left(số\right)\)

Chọn 4 chữ số còn lại : \(C^4_6\)
Số số cần tìm : \(\dfrac{C^4_6\cdot7!}{3!}\)
Đáp án A
Thêm vào hai chữ số 1 vào tập hợp các chữ số đã cho ta được tập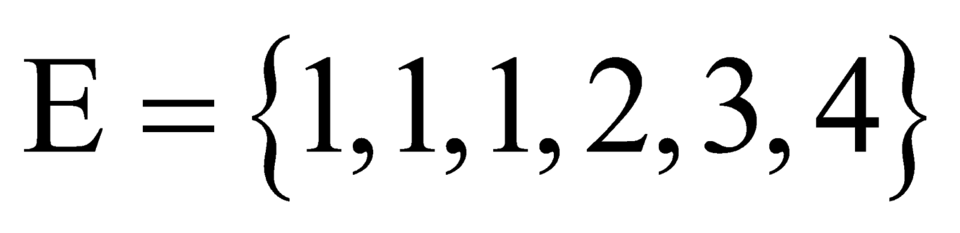
Xem các số 1 là khác nhau thì mỗi hoán vị của 6 phần tử của E cho ta một số có 6 chữ số thỏa mãn bài toán. Như vậy ta có 6! số. Tuy nhiên khi hoán vị vủa ba số 1 cho nhau thì giá trị con số không thay đổi nên mỗi số như vậy ta đếm chúng đến 3! lần.
Vậy số các số thỏa mãn yêu cầu bài toán là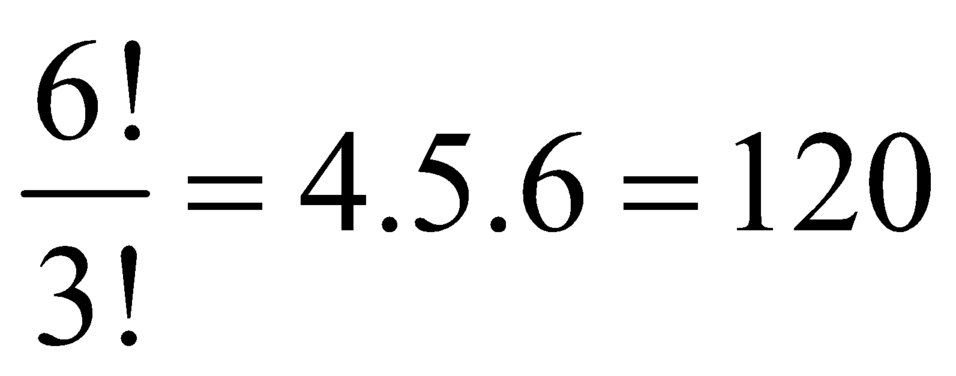 số.
số.
Chú ý: Ta có thể giải như sau, ta gọi số 6 chữ số cần tìm là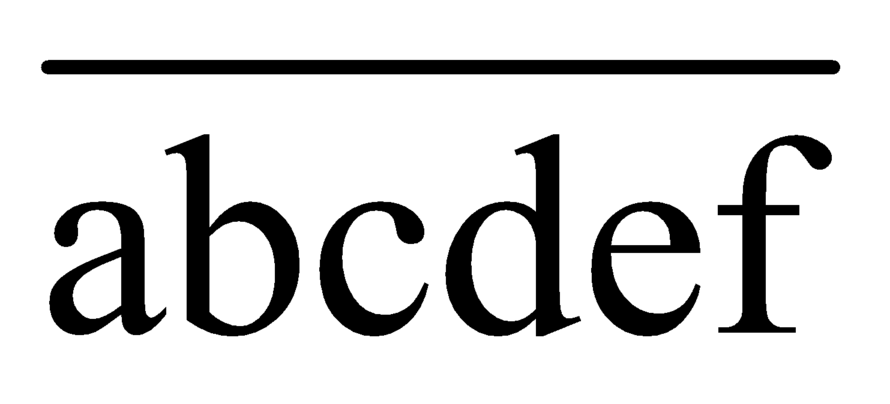 , chọn 3 vị trí trong 6 vị trí để đặt ba chữ số 1 có
, chọn 3 vị trí trong 6 vị trí để đặt ba chữ số 1 có  cách, xếp 3 chữ số 2,3,4 vào ba vị trí còn lại có 3! cách do đó
cách, xếp 3 chữ số 2,3,4 vào ba vị trí còn lại có 3! cách do đó