Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD. M là điểm trên cạnh BC sao cho MB=2MC. Khi đó đường thẳng MG song song với mặt phẳng nào dưới đây?
A. (ACD)
B. (BCD)
C. (ABD)
D. (ABC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

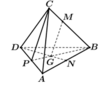
Gọi P là trung điểm của AD.
Vì G là trọng tâm tam giác BCD nên 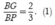
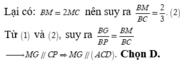

Đáp án D
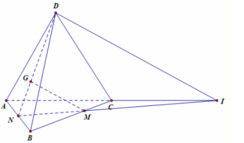
Gọi N là trung điểm của AB.Trong mặt phẳng (ABC)
gọi I là giao điểm của MN và AC.Ta có N G N D = N M N I = 1 3 ⇒ G M / / D I
Mà D I ⊂ A C D ⇒ G M / / A C D .

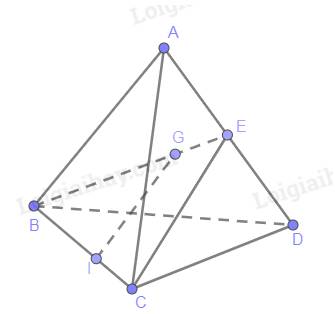
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)

Đáp án B
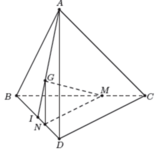
Lấy điểm N trên cạnh BD sao cho NB = 2ND. Khi đó ta có M N | | D C .
Gọi I là trung điểm BD ta có G ∈ A I và I G = 1 3 I A .
Mặt khác ta có D N = 1 3 D B = 2 3 D I ⇒ I N = 1 3 I D .
Từ (2) và (3) suy ra N G | | A D .
Từ (1) và (4) suy ra G M N | | A C D do đó G M | | A C D
Nhận xét: Có thể loại các đáp án sai bằng cách nhận xét đường thẳng GM cắt các mặt phẳng (BCD), (ABD), (ABC).
Chọn A