Trong không gian cho hình thang cân ABCD có AB//CD, AB = a,CD = 2a,AD = a Gọi M, N lần lượt là trung điểm của AB và CD. Gọi K là khối tròn xoay được tạo ra khi xoay hình thang ABCD quanh trục MN. Tính thể tích V của khối K.
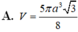
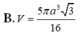
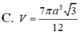
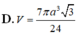
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

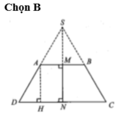
Gọi S là giao điểm của AD và BC. Nếu quay tam giác SCD quanh trục SN, các đoạn thẳng SC. SB lần lượt tạo ra mặt xung quanh của hình nón ( H 1 ) v à ( H 2 ) .
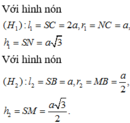

Đáp án D
Khi quay hình thang cân ABCD quanh trục đối xứng ta được hình nón cụt có chiều cao h = 2 a 2 và bán kính 2 đáy là R 1 = a , R 2 = 2 a .
Vậy thể tích cần tính là V = πh 3 R 1 2 + R 2 2 + R 1 R 2 = 14 2 3 πa 3
Chọn D