Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Áp dụng bất đẳng thức vectơ
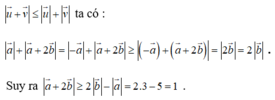
Dấu bằng xảy ra khi 2 vectơ 
cùng hướng. Vậy độ dài của vectơ |
a
→
-
2
b
→
| ≥ 0 nhỏ nhất bằng 1.
Suy ra đáp án đúng là C.
Gọi M a ; b ; N c ; d
Khi đó ta có M thuộc đường tròn x - 1 2 + y - 2 2 = 1 C và N thuộc đường thẳng
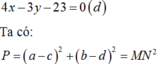
Đường tròn (C) có tâm I 1 ; 2 , bán kính R = 1
Ta có
Khi đó
Chọn D.
Áp dụng bất đẳng thức Cauchy cho 2 số dương ta có:
a 2 + b 2 ≥ 2 a b , b 2 + c 2 ≥ 2 b c , c 2 + a 2 ≥ 2 c a
Do đó: 2 a 2 + b 2 + c 2 ≥ 2 ( a b + b c + c a ) = 2.9 = 18 ⇒ 2 P ≥ 18 ⇒ P ≥ 9
Dấu bằng xảy ra khi a = b = c = 3 . Vậy MinP= 9 khi a = b = c = 3
Vì a , b , c ≥ 1 , nên ( a − 1 ) ( b − 1 ) ≥ 0 ⇔ a b − a − b + 1 ≥ 0 ⇔ a b + 1 ≥ a + b
Tương tự ta có b c + 1 ≥ b + c , c a + 1 ≥ c + a
Do đó a b + b c + c a + 3 ≥ 2 ( a + b + c ) ⇔ a + b + c ≤ 9 + 3 2 = 6
Mà P = a 2 + b 2 + c 2 = a + b + c 2 − 2 a b + b c + c a = a + b + c 2 – 18
⇒ P ≤ 36 − 18 = 18 . Dấu bằng xảy ra khi : a = 4 ; b = c = 1 b = 4 ; a = c = 1 c = 4 ; a = b = 1
Vậy maxP= 18 khi : a = 4 ; b = c = 1 b = 4 ; a = c = 1 c = 4 ; a = b = 1
Đáp án B
Từ giả thiết suy ra 
Do đó AB ≥ |OA - OB| = 1. Dấu bằng xảy ra khi O nằm ngoài đoạn AB. Suy ra đáp án đúng là B.
Hai đáp án A, D sai do nhầm OA = x 2 + y 2 + z 2 = 4; OB = m 2 + n 2 + p 2 = 9
Đáp án C sai do nhầm với câu hỏi vectơ AB→ có độ dài lớn nhất
Do \(a\ge1;b\ge1;c\ge1\left(nên\right)\)
\(\left(a-1\right)\left(b-1\right)+\left(b-1\right)\left(c-1\right)+\left(c-1\right)\left(a-1\right)\ge0\)
\(\Leftrightarrow ab+bc+ac+3\ge2\left(a+b+c\right)\Leftrightarrow a+b+c\le5\)
khi đó \(P=3a+2b+c-1=3\left(a+b+c\right)-\left(b+2c\right)-1\le15-3-1=11\)
dấu = xảy ra khi a=3 , b=c=1
=> GTLN(P)=11
Mặt khác \(\left(a+b\right)\left(a+c\right)=ab+bc+ca+a^2\ge8\)
nên ta có \(P=2\left(a+b\right)\left(a+c\right)-1\ge2\sqrt{2\left(a+b\right)\left(a+c\right)}\ge2\sqrt{16}-1=7\)
dấu = xảy ra khi a=b=1, c=3
zậy ..
Ta có: 2P=(a2+b2) + (b2+c2) + (c2+a2)
Theo Cauchy có:
\(2P\ge2ab+2bc+2ca=2\left(ab+bc+ca\right)=2.9\)
=> \(P\ge9\)=> Pmin = 9 đạt được khi x=y=\(\sqrt{3}\)
Hoặc:
P2= (a2+b2+c2)(b2+c2+a2)
Theo Bunhiacopxki có:
P2= (a2+b2+c2)(b2+c2+a2) \(\ge\)(ab+bc+ca)2=92
=> P\(\ge\)9 => Pmin=9
Vì \(a\ge1,b\ge1,c\ge1\)(gt) => \(\left(a-1\right)\left(b-1\right)\ge0\)<=> ab -a -b + 1 \(\ge0\)(1)
\(\left(b-1\right)\left(c-1\right)\ge0\)<=> bc - b - c + 1 \(\ge0\)(2)
\(\left(c-1\right)\left(a-1\right)\ge0\)<=> ca -c - a + 1 \(\ge0\)(3)
Cộng từng vế của (1), (2) và (3) ta được:
ab + bc + ca -2(a +b +c) + 3 \(\ge0\)
=> \(a+b+c\le\frac{ab+bc+ca+3}{2}=\frac{9+3}{2}=6\)
Mà \(a\ge1,b\ge1,c\ge1\Rightarrow a+b+c\ge3\)=> \(3\le a+b+c\le6\)=> \(\left(a+b+c\right)^2\le36\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)\le36\)
=> \(a^2+b^2+c^2\le36-2\left(ab+bc+ca\right)=36-2\times9=18\)=> P \(\le18\)
Vậy GTLN của P là 18
Dâu "=" xảy ra khivà chỉ khi:
a =b=1, c=4
hoặc: b=c=1, a=4
hoặc: c=a=1, b=4
Do vai trò của \(a,b\)là như nhau nên giả sử \(a\ge b\).
Ta có nhận xét rằng \(ab\)lớn nhất khi giá trị của \(a\)và \(b\)bằng nhau hoặc \(a-b=1\).
Nếu \(a-b>1\): ta thay tích \(ab\)bởi tích \(\left(a-1\right)\left(b+1\right)\)được
\(\left(a-1\right)\left(b+1\right)-ab=ab+a-b-1-ab=a-b-1>0\)
do đó \(a-b\le1\).
Vì \(a,b\)là số tự nhiên mà \(a+b=2019\)là số lẻ nên \(P\)đặt max tại \(a-b=1\)
\(\Rightarrow\hept{\begin{cases}a=1010\\b=1009\end{cases}}\).
Vậy \(maxP=1010.1009\).
\(P=2\Sigma a+\Sigma\dfrac{1}{a}=\Sigma a+\Sigma a+\Sigma\dfrac{1}{a}\ge3.\sqrt[3]{\left(\Sigma a\right)^2.\Sigma\dfrac{1}{a}}\)
\(Q=\left(\Sigma a\right)^2.\Sigma\dfrac{1}{a}=\left(3+2\Sigma ab\right).\Sigma\dfrac{1}{a}=3\Sigma\dfrac{1}{a}+4\Sigma a+2\Sigma\dfrac{ab}{c}\ge3\Sigma\dfrac{1}{a}+6\Sigma a=3\left(\Sigma\dfrac{1}{a}+2\Sigma a\right)=3P\)\(\Rightarrow\)\(P\ge3\sqrt[3]{3P}\) \(\Leftrightarrow P^3\ge81P\Leftrightarrow P^2\ge81\left(P>0\right)\Leftrightarrow P\ge9\)
" = " \(\Leftrightarrow a=b=c=1\)
Vì $\large a,b,c \in\mathbb{N^*}$ và $\large a^2+b^2+c^2=3\Rightarrow \left\{\begin{matrix} a<\sqrt{3} & \\ b<\sqrt{3} & \\ c<\sqrt{3} & \end{matrix}\right.$
Ta chứng minh bất đẳng thức phụ sau:
Với $0 <x<\sqrt{3}$ thì $2x+\frac{1}{x} \ge x^2.\frac{1}{2}+\frac{5}{2}(*)$
Thật vậy $(*)$ $\large \Leftrightarrow (x-2)(x-1)^2 \le0$
Do $\large x<\sqrt{3}\Leftrightarrow x<2\Leftrightarrow (x-2)(x-1)^2<0$ (Luôn đúng)
Do đó bất đẳng thức được chứng minh
Dấu $"="$ xảy ra khi $x=1$
Trở lại bài toán:
Áp dụng BĐT $(*)$ ta được:
$\large 2a+\frac{1}{a}+2b+\frac{1}{b}+2c+\frac{1}{c}\ge\frac{1}{2}(a^2+b^2+c^2)+\frac{15}{2}=9$
Do $a^2+b^2+c^2=3$
Vậy $GTNN=9$
Dấu $"="$ xảy ra khi: $a=b=c=1$
Đáp án A
Sử dụng bất đẳng thức vectơ:
Dấu bằng xảy ra khi và chỉ khi hai vectơ này ngược hướng. Suy ra đáp án A.
Hai đáp án B và C xuất phát từ sai lầm