Vẽ hình tứ giác có 2 góc vuông.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Bài 2:
a: \(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\widehat{CFE}=60^0\\\widehat{AEB}=\widehat{CEF}=60^0\end{matrix}\right.\)
=>ΔCFE đều
b: Xét tứ giác ABCD có
\(\widehat{BAC}=\widehat{BDC}=90^0\)
Do đó: ABCD là tứ giác nội tiếp

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
b: Xét tứ giác ADEN có
NE//AD
NE=AD
Do đó: ADEN là hình bình hành

a) Xét tứ giác AEMF có
\(\widehat{EAF}=90^0\)(gt)
\(\widehat{AEM}=90^0\)(gt)
\(\widehat{AFM}=90^0\)(gt)
Do đó: AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Xét ΔABC có
M là trung điểm của BC(gt)
MF//AB(cùng vuông góc với AC)
Do đó: F là trung điểm của AC(Định lí 1 về đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
F là trung điểm của AC(cmt)
Do đó: MF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: \(MF=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà AE=MF(AFME là hình chữ nhật)
nên \(AE=\dfrac{AB}{2}\)
mà A,E,B thẳng hàng(gt)
nên E là trung điểm của AB
Ta có: F là trung điểm của NM(gt)
nên \(MN=2\cdot MF\)(1)
Ta có: E là trung điểm của AB(cmt)
nên AB=2AE(2)
Ta có: AEMF là hình chữ nhật(cmt)
nên MF=AE(Hai cạnh đối)(3)
Từ (1), (2) và (3) suy ra MN=AB
Xét tứ giác ABMN có
MN//AB(cùng vuông góc với AC)
MN=AB(cmt)
Do đó: ABMN là hình bình hành(Dấu hiệu nhận biết hình bình hành)

a: Xét tứ giác AEID có
góc AEI=góc ADI=góc DAE=90 độ
nên AEID là hình chữ nhật
b: Xét ΔBAC co DI//AC
nên DI/AC=BI/BC=BD/BA=1/2
=>D là trung điểm của AB
Xét ΔBAC có EI//AB
nên EI/AB=CI/CB=CE/CA=1/2
=>E là trung điểm của AC
=>DI//CE và DI=CE
=>DICE là hình bình hành
c: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>DE//IH
ΔHAC vuông tại H
mà HE là trung tuyến
nên HE=AC/2=DI
Xét tứ giác IHDE có
IH//DE
ID=HE
Do đó: IHDE là hình thang cân

Bài làm
Theo hình,
Góc A là góc nhọn
Góc B là góc tù
góc C là góc vuông
Góc D là góc tù

a)
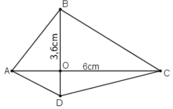
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài. Chẳng hạn tứ giác ABCD ở hình trên.
Ta có: AC = 6cm, BD = 3,6cm và AC ⊥ BD.
Diện tích tứ giác ABCD là:
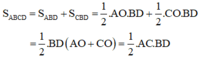
Mà AC = 6cm ; BD = 3,6 cm nên 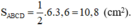
b) Hình vuông có 2 đường chéo vuông góc nên theo công thức trên, diện tích của nó là: