Cho đường tròn tâm O bán kính 3 cm và hai dây AB và AC. Biết AB = 5cm, AC = 2cm. Trong 2 dây AB và AC dây nào gần tâm hơn?
A. AB
B. AC
C. Chưa thể kết luận được
D. Hai dây cách đều tâm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

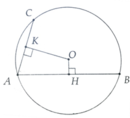
Gọi OH,OK Lần lượt là khoảng cách từ O đến AB,AC
Tính được OH = 41 2 cm và OH = 2 2 cm

Đáp án B
Áp dụng định lí Pytago vào tam giác ABC ta có:
B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100 nên BC =10 cm
Ta có: AB < AC < BC ( 6 cm < 8 cm < 10 cm )
Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất

Đáp án C
Tam giác ABC có góc A là góc tù nên 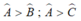
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.

mình nghĩ bạn nên sửa CD thành AC bạn nhé do ko có D á
a, Ta có d(O;AB) = OI
d(O;AC) = OJ
mà AB > AC ( 5 cm > 2 cm )
=> OT < OJ
b, Vì OI vuông AB => I là trung điểm AB
=> IB = AB/2 = 5/2 cm
Theo định lí Pytago tam giác OIB vuông tại I
\(OB^2=IB^2+OI^2\Rightarrow OI^2=OB^2-IB^2=9-\frac{25}{4}=\frac{36-25}{4}=\frac{11}{4}\Rightarrow OI=\frac{\sqrt{11}}{2}\)cm
Vì OJ vuông AC => J là trung điểm AC
=> JA = AC/2 = 1 cm
Theo định lí Pytago cho tam giác OAJ vuông tại J
\(AO^2=JO^2+JA^2\Rightarrow JO^2=AO^2-JA^2=9-1=8\Rightarrow JO=2\sqrt{2}\)cm

a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)
Đáp án A
Ta có: AB > AC ( 5 cm > 3 cm) nên dây AB gần tâm hơn.