Cho hàm số f x = x 2 − 3 x + 2 x − 1 khi x ≠ 1 a khi x = 1 . Tìm a để f(x) liên tục trên ℝ .
A. -1
B. 1
C. Không tồn tại giá trị của a
D. 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: TXĐ: D=R
b: \(f\left(-1\right)=\dfrac{2}{-1-1}=\dfrac{2}{-2}=-1\)
\(f\left(0\right)=\sqrt{0+1}=1\)
\(f\left(1\right)=\sqrt{1+1}=\sqrt{2}\)
\(f\left(2\right)=\sqrt{3}\)
Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.
Đáp án C
Do y ' chỉ đổi dấu tại x = -2, x = 3. Nên hàm số đã cho có 2 điểm cực trị
a: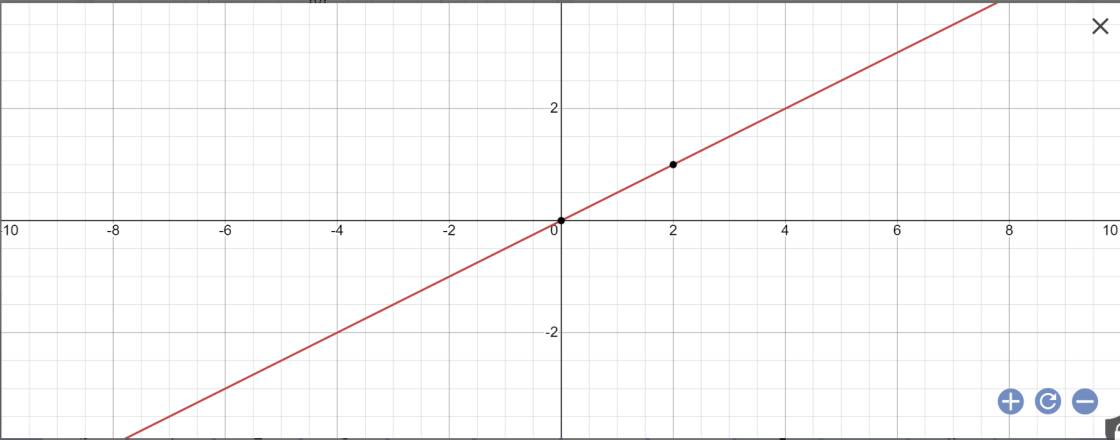 
b: \(f\left(2\right)=\dfrac{1}{2}\cdot2=1\)
\(f\left(1\right)=\dfrac{1}{2}\cdot1=\dfrac{1}{2}\)
\(f\left(-2\right)=\dfrac{1}{2}\cdot\left(-2\right)=-1\)
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\)
\(f\left(0\right)=\dfrac{1}{2}\cdot0=0\)
c: f(x)=2
=>\(\dfrac{1}{2}x=2\)
=>x=2*2=4
f(x)=1
=>\(\dfrac{1}{2}x=1\)
=>\(x=1:\dfrac{1}{2}=2\)
f(x)=-1
=>\(\dfrac{1}{2}x=-1\)
=>\(x=-1\cdot2=-2\)
d: \(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\ne\dfrac{1}{2}=y_A\)
=>A(-1;1/2) không thuộc đồ thị hàm số y=1/2x
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}=y_B\)
=>\(B\left(-1;-\dfrac{1}{2}\right)\) thuộc đồ thị hàm số y=1/2x
Chọn C.
Hàm số đã cho các định trên R \ {2}.
Ta có 
Đặt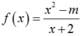 
khi x < 3 (m là tham số, m > 0).
Ta có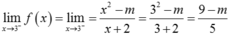 
.
Để hàm số f(x) có giới hạn khi x → 3 thì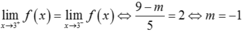 
.