Cho biểu thức 5x2 + 3x – 1. Tính giá trị của biểu thức tại: x = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
5 tháng 10 2019
Thay x = -1 vào biểu thức, ta có:
5.(-1)2 + 3.(-1) – 1 = 5.1 – 3 – 1 = 1
Vậy giá trị của biểu thức 5x2 + 3x – 1 tại x = -1 là 1
PT
1
CM
4 tháng 6 2018
Thay x = 1/3 vào biểu thức, ta có:
5.(1/3)2 + 3.1/3 – 1 = 5.1/9 + 1 – 1 = 5/9
Vậy giá trị của biểu thức 5x2 + 3x – 1 tại x = 1/3 là 5/9
28 tháng 3 2018
a. Thay x = 0 vào biểu thức, ta có:
5.02 + 3.0 – 1 = 0 + 0 – 1 = -1
Vậy giá trị của biểu thức 5x2 + 3x – 1 tại x = 0 là -1
b. Thay x = -1 vào biểu thức, ta có:
5.(-1)2 + 3.(-1) – 1 = 5.1 – 3 – 1 = 1
Vậy giá trị của biểu thức 5x2 + 3x – 1 tại x = -1 là 1
c. Thay x = 13 vào biểu thức, ta có:
5.(1/3)2 + 3.1/3 – 1 = 5.1/9 + 1 – 1 = 5/9
Vậy giá trị của biểu thức 5x2 + 3x – 1 tại x = 1/3 là 5/9
28 tháng 3 2018
a) Thay x = 0 vào biểu thức ta có:
5.02+3.0−1=0+0−1=−15.02+3.0−1=0+0−1=−1
Vậy giá trị của biểu thức 5x2+3x−15x2+3x−1 tại x = 0 là -1
b) Thay x = -1 vào biểu thức ta có:
5.(−1)2+3.(−1)−1=5.1−3−1=15.(−1)2+3.(−1)−1=5.1−3−1=1
Vậy giá trị của biểu thức 5x2+3x−15x2+3x−1 tại x = -1 là 1.
c) Thay x=13x=13 vào biểu thức ta có:
5.(13)2+3.13−1=5.19+1−1=595.(13)2+3.13−1=5.19+1−1=59
Vậy giá trị của biểu thức 5x2+3x−15x2+3x−1 tại x=13x=13 là 59
PT
1
CM
22 tháng 9 2019
Thay x = -2 vào biểu thức A ta có
A = 5.(-2)2 - 3.(-2) - 16 = 10 (1 điểm)
1 tháng 11 2023
Sửa đề: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{{}\begin{matrix}2x+2y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x-y\right)^{2023}-\left(x-2\right)^{2024}+\left(y+1\right)^{2023}\)
\(=\left(1+1\right)^{2023}-\left(1-2\right)^{2024}+\left(-1+1\right)^{2023}\)
\(=2^{2023}-1\)
TD
2
KV
26 tháng 8 2023
Thay x = 4 vào A ta được:
5.4⁵ - 5.4⁴ + 5.4³ - 5.4² + 5.4 - 1
= 5.1024 - 5.256 + 5.64 - 5.16 + 5.4 - 1
= 5120 - 1280 + 320 - 80 + 20 - 1
= 4099
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$
13 tháng 11 2021
\(a,ĐK:x\ne-3;x\ne0;y\ne0\\ b,A=\dfrac{1}{x^2\left(x+3\right)+y^2\left(x+3\right)}=\dfrac{1}{\left(x^2+y^2\right)\left(x+3\right)}\\ x=y=0\Leftrightarrow A\in\varnothing\)
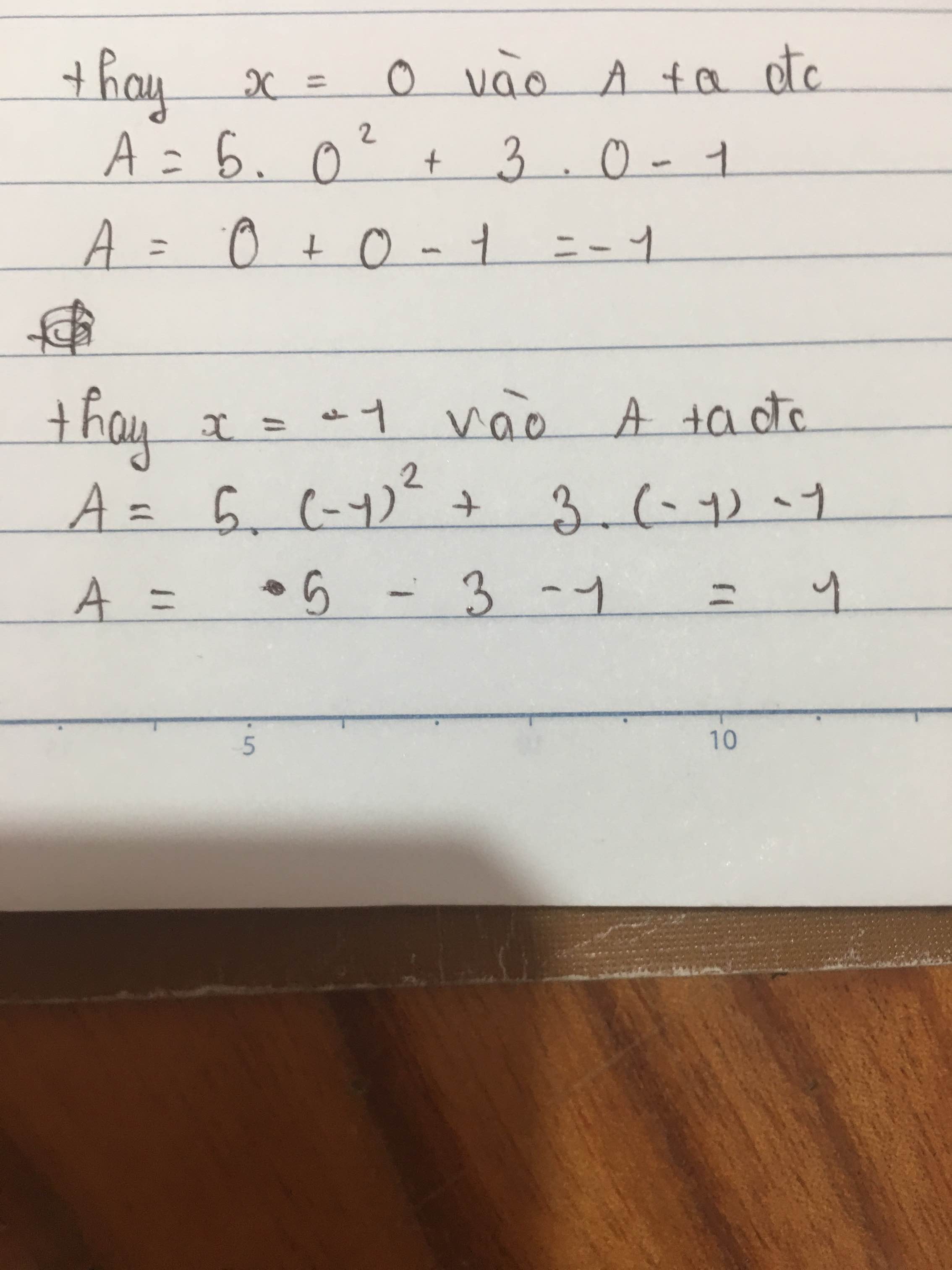
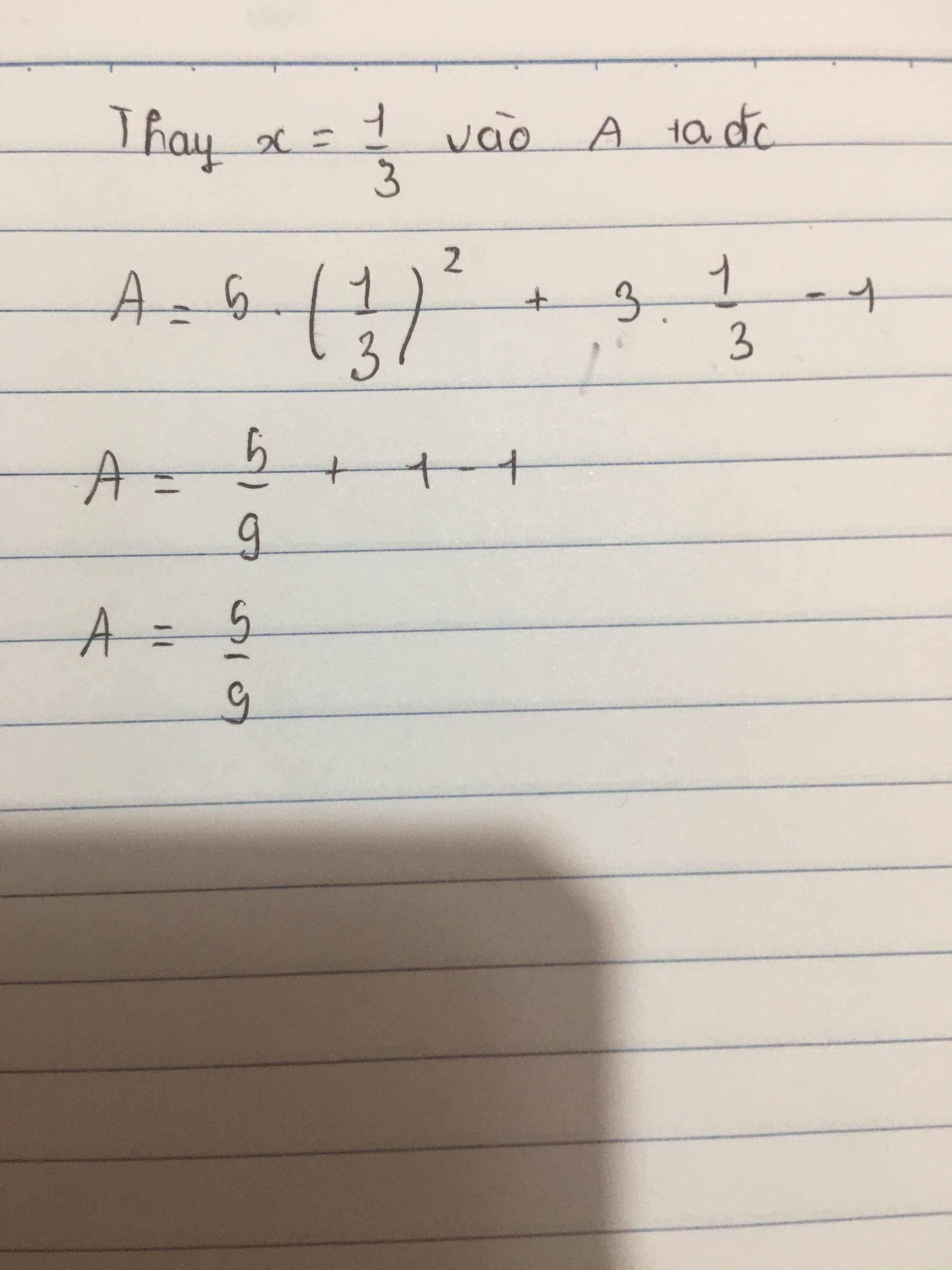
Thay x = 0 vào biểu thức, ta có:
5.02 + 3.0 – 1 = 0 + 0 – 1 = -1
Vậy giá trị của biểu thức 5x2 + 3x – 1 tại x = 0 là -1