Tìm đa thức A biết: A – (xy + x2 – y2) = x2 + y2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A + (x2 + y2) = 5x2 + 3y2 – xy
A = 5x2 + 3y2 – xy - (x2 + y2)
= 5x2 + 3y2 – xy - x2 - y2
= (5x2 – x2) + (3y2 – y2) – xy
= 4x2 + 2y2 - xy

a: Sửa đề: \(2A+\left(2x^2+y^2\right)=6x^2+5y^2-2x^2y^2\)
=>\(2A=6x^2+5y^2-2x^2y^2-2x^2-y^2\)
=>\(2A=4x^2+4y^2-2x^2y^2\)
=>\(A=2x^2+2y^2-x^2y^2\)
b: \(2A-\left(xy+3x^2-2y^2\right)=x^2-8y+xy\)
=>\(2A=x^2-8y+xy+xy+3x^2-2y^2\)
=>\(2A=4x^2+2xy-8y-2y^2\)
=>\(A=2x^2+xy-4y-y^2\)
c: Sửa đề: \(A+\left(3x^2y-2xy^2\right)=2x^2y+4xy^3\)
=>\(A=2x^2y+4xy^3-3x^2y+2xy^2\)
=>\(A=-x^2y+4xy^3+2xy^2\)

a) \(=3\left(x^2-10x+25\right)=3\left(x-5\right)^2\)
b) \(=x\left(x+y\right)+8\left(x+y\right)=\left(x+y\right)\left(x+8\right)\)
c) \(=\left(x+2\right)^2-y^2=\left(x+2-y\right)\left(x+2+y\right)\)

A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2

a) (x + 2)(x + 4). b) 2(x + 6)(x + l).
c) 3(3x + 5)(x + l). d) (6x -7y)(x + y).

P + (x2 – 2y2) = x2 - y2 + 3y2 – 1
⇒ P = (x2 – y2 + 3y2 – 1) – (x2 – 2y2)
= x2 – y2 + 3y2 – 1 – x2 + 2y2
= (x2 – x2) + ( – y2 + 3y2+ 2y2) – 1
= 0+ 4y2 – 1= 4y2 – 1.
Vậy P = 4y2 – 1.

a: \(=4xy\left(1-5x^2y\right)\)
b: \(=\left(x-y\right)\left(x+y\right)+3\left(x-y\right)=\left(x-y\right)\left(x+y+3\right)\)
c: \(=x\left(x-a\right)+y\left(x-a\right)=\left(x-a\right)\left(x+y\right)\)
d: \(=\left(x+2y\right)^2-36=\left(x+2y+6\right)\left(x+2y-6\right)\)
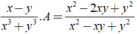
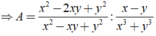
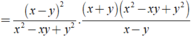
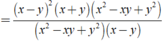
A – (xy + x2 – y2) = x2 + y2
A = (x2 + y2) + (xy + x2 – y2)
= x2 + y2 + xy + x2 – y2
= (x2 + x2) + (y2 – y2) + xy
= 2x2 + xy