Cho đường tròn tâm O, hai dây AB và CD vuông góc với nhau ở M. Biết AB = 18 cm, CD = 14 cm, MC =4 cm. Hãy tính khoảng cách từ tâm O đến mỗi dây AB và CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 7 2017
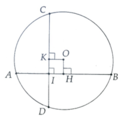
Gọi OH,OK là khoảng cách từ O đến mỗi dây
Ta có: OH = OK = 1cm
Tính được R = 10 cm
CM
28 tháng 3 2019
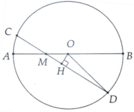
a, Gọi OH là khoảng cách từ O đến CD => MH = 4cm
Tính được OH = 4 3 3 cm
b, Tính được OD = 4 39 3 cm
24 tháng 3 2021
a) Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
\(\widehat{BCD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
Do đó: \(\widehat{BAD}=\widehat{BCD}\)(Hệ quả góc nội tiếp)
hay \(\widehat{IAD}=\widehat{ICB}\)
Xét ΔIAD và ΔICB có
\(\widehat{IAD}=\widehat{ICB}\)(cmt)
\(\widehat{AID}=\widehat{CIB}\)(hai góc đối đỉnh)
Do đó: ΔIAD\(\sim\)ΔICB(g-g)
Suy ra: \(\dfrac{IA}{IC}=\dfrac{ID}{IB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(IA\cdot IB=IC\cdot ID\)(đpcm)
Gọi H và K lần lượt là hình chiếu của O trên AB và CD
Tính được OH = MK = 3cm
OD = OB = 3 10 cm
Từ đó tính được OK = 41 cm