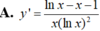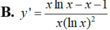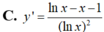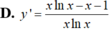Tìm đạo hàm của hàm số sau: y = x + 1 x + 0 , 1 . x 10
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 8 2019
Đúng(0)
Những câu hỏi liên quan
PT
1
PT
1
PT
1
PT
1
CM
15 tháng 7 2018
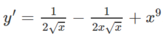
y ′ = − 1 − x 2 ( 1 − x 2 ) 1 − x 3 2 ( 1 + 6 x + 15 x 2 + 14 x 3 )
CM
30 tháng 5 2018
a) Hàm hằng ⇒ Δy = 0
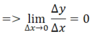
b) theo định lí 1
y = x hay y = x1 ⇒ y’= (x1)’= 1. x1-1 = 1. xo = 1.1 =1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
Để hàm số có đạo hàm tại 1 điểm thì nó phải liên tục tại điểm đó đồng thời đạo hàm trái bằng đạo hàm phải
\(\lim\limits_{x\rightarrow0^-}\left(2ax+1\right)=1\)
\(\lim\limits_{x\rightarrow0^+}\left(x^2+ax+1\right)=1\)
\(\Rightarrow\) Hàm liên tục tại \(x=1\)
\(y'\left(0^+\right)=2a\)
\(y'\left(0^-\right)=\left(2x+a\right)_{x=0^-}=a\)
Hàm có đạo hàm tại x=0 \(\Leftrightarrow2a=a\Leftrightarrow a=0\)
CM
19 tháng 12 2018
y’= -2f’(x) nên hàm số nghịch biến trên (-∞;-2),(-1;2) và (4;+∞).
Chọn đáp án B.
PT
1
