Cho hình bình hành ABCD, M là trung điểm của cạnh BC. Tia AM cắt tia DC tại điểm E. Chứng minh SABCD = SAED.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2020
+) Kẻ: AJ // CI //EF; I; J thuộc BD và M thuộc EF
Xét \(\Delta\)BAJ có: FM // AJ
=> \(\frac{BA}{BF}=\frac{BJ}{BM}\)
Xét \(\Delta\)BCI có: ME // IC
=> \(\frac{BC}{BE}=\frac{BI}{BM}\)
Từ hai điều trên => \(\frac{BA}{BF}+\frac{BC}{BE}=\frac{BJ}{BM}+\frac{BI}{BM}=\frac{BI+BJ}{BM}\)(1)
Xét \(\Delta\)AJO và \(\Delta\)CIO có:
OA = OC ( ABCD là hình bình hành)
^AOJ = ^COI ( đối đỉnh)
^AJO = ^CIO ( AJ // CI , so le trong )
=> \(\Delta\)AJO = \(\Delta\)CIO ( g-c-g)
=> JO = IO
KHi đó BI + BJ = BO + OI + BO - JO = 2 BO + (IO - JO) = 2 BO = 2.2. BM = 4BM ( vì M là trung điểm BO )
=> BI + BJ = 4BM Thế vào (1)
=> \(\frac{BA}{BF}+\frac{BC}{BE}=\frac{4BM}{BM}=4\)(2)
+) Kẻ BH // BG //FK với H; G thuộc AC
Chứng minh tương tự như trên ta suy ra: \(\frac{BA}{AF}+\frac{AD}{AK}=4\)(3)
Cộng (2) + (3) vế theo vế:
\(\frac{BA}{BF}+\frac{BC}{BE}+\frac{BA}{AF}+\frac{AD}{AK}=8\)mà AD = BC
=> \(AB\left(\frac{1}{BF}+\frac{1}{AF}\right)+BC\left(\frac{1}{BE}+\frac{1}{AK}\right)=8\)(4)
Mặt khác: \(\frac{1}{BF}+\frac{1}{AF}=\frac{1^2}{BF}+\frac{1^2}{AF}\ge\frac{\left(1+1\right)^2}{BF+AF}=\frac{4}{AB}\) và \(\frac{1}{BE}+\frac{1}{AK}\ge\frac{4}{BE+AK}\)
KHi đó: \(8\ge AB.\frac{4}{AB}+BC.\frac{4}{BE+AK}\)
<=> \(BE+AK\ge BC\)
Dấu "=" xảy ra <=> BF = AF và BE = AK
Hay F là trung điểm AB.
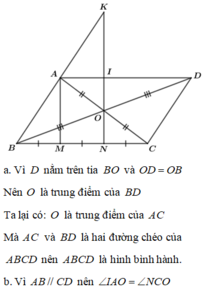
Chứng minh DABM = DECM
Chứng minh SABM - SECM'
Þ SABCD = SAED