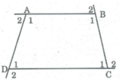
Tính tổng các góc ngoài của tứ giác (tai mỗi đỉnh của tứ giác chỉ chọn một góc ngoài).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) + Góc ngoài tại A là góc A1:
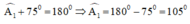
+ Góc ngoài tại B là góc B1:
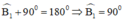
+ Góc ngoài tại C là góc C1:

+ Góc ngoài tại D là góc D1:
Theo định lý tổng các góc trong một tứ giác bằng 360º ta có:
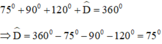
Lại có:
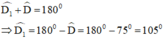
Vậy góc ngoài tại D bằng 105º.
b) Hình 7b:
Ta có:
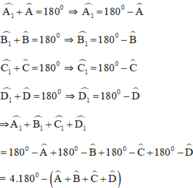
Mà theo định lý tổng bốn góc trong một tứ giác bằng 360º ta có:
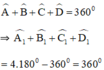
c) Nhận xét: Tổng các góc ngoài của tứ giác cũng bằng 360º.

4 góc tứ giác là a,b,c,d
=.4 góc ngoài =180-a,180-b,180-c,180-d
=>tổng chúng =720độ - 360 độ=360 độ
Gọi 4 góc của tứ giác là : a , b , c , d
Thì 4 góc ngoài của tứ giác lần lượt là : 180 - a ; 180 - b ; 180 - c ; 180 - d
Vậy 4 góc ngoài của tứ giác là : 180 - a + 180 - b + 180 - c + 180 - d
= ( 180 + 180 + 180 + 180 ) - ( a + b + c + d )
= 720o - 360o ( tổng 4 góc của tứ giác )
= 360o
Vậy tổng 4 góc ngoài của tứ giác là 360o


Bài giải:
a) Góc ngoài còn lại: 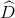 =3600 – (750 + 900 + 1200) = 750
=3600 – (750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là:
1050, 900, 600, 1050
b)Hình 7b SGK:
Tổng các góc trong  +
+  +
+ +
+ =3600
=3600
Nên tổng các góc ngoài
 +
+  +
+ +
+ =(1800 -
=(1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  )
)
=(1800.4 - ( 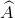 +
+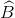 +
+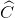 +
+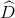 )
)
=7200 – 3600 =3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
\(\Leftrightarrow\widehat{D}=360^o-\left(90^o+120^o+75^o\right)\)
\(\Leftrightarrow\widehat{D}=360^o-285^o=75^o\)
Ta có:+)\(\widehat{BAD}+\widehat{A_1}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{A_1}=180^o-\widehat{BAD}\)
\(\Rightarrow\widehat{A_1}=180^o-75^o=105^o\)
+)\(\widehat{B}_1+\widehat{CBA}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-\widehat{CBA}\)
\(\Rightarrow\widehat{B_1}=180^o-90^0=90^o\)
\(+)\widehat{C_1}+\widehat{BCD}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{C_1}=180^o-\widehat{BCD}\)
\(\Rightarrow\widehat{C_1}=180^o-120^o=60^o\)
\(+)\widehat{D_1}+\widehat{ADC}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{D}_1=180^o-\widehat{ADC}\)
\(\Rightarrow\widehat{D_1}=180^o-75^o=105^o\)
b,Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}+\widehat{D_1}\)
\(=\left(180^o-\widehat{A}\right)+\left(180^o-\widehat{B}\right)+\left(180^o-\widehat{C}\right)+\left(180^o-\widehat{D}\right)\)
\(=180^o.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(=720^o-360^o=360^o\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^o\)

a) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của tứ giác (lồi) là 1800 Þ Tổng số đo các góc trong và các góc ngoài của tứ giacs là 4.1800 = 7200.
Mặt khác, tổng số đo các góc trong của tứ giác là: (4-2).1800 = 3600.
Þ Tổng số đo các góc ngoài của tứ giác là: 7200 - 3600 = 3600
Tương tự, ta cũng tính được tổng số đo các góc ngoài của ngũ giác và thập giác là 3600.
b) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n - giác (lồi) là 1800 Þ Tổng số đo các góc trong và các góc ngoài của đa giác là n.1800.
Mặt khác, tổng số đo các góc trong của đa giác là (n - 2).1800.
Þ Tổng số đo các góc ngoài của đa giác là:
n.1800 - (n - 2).1800 = 3600.

Trong tứ giác \(ABCD\) có: \(\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC} = 360^\circ \)
Ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\\)
\(= \left( {180^\circ - \widehat {DAB}} \right) + \left( {180^\circ - \widehat {ABC}} \right) + \left( {180^\circ - \widehat {BCD}} \right) + \left( {180^\circ - \widehat {ADC}} \right)\\\)
\(= 180^\circ + 180^\circ + 180^\circ + 180^\circ - \left( {\widehat {DAB} + \widehat {ABC} + \widehat {BCD} + \widehat {ADC}} \right)\\ \)
\(= 720^\circ - 360^\circ \\\)
\(= 360^\circ \)
Ta có: ∠ A 1 + ∠ B 1 + ∠ C 1 + ∠ D 1 = 360 o (tổng các góc của tứ giác)
+) Lại có: ∠ A 1 + ∠ A 2 = 180 o ( hai góc kề bù).
∠ B 1 + ∠ B 2 = 180 o (hai góc kề bù)
∠ C 1 + ∠ C 2 = 180 o (hai góc kề bù)
∠ D 1 + ∠ D 2 = 180 o (hai góc kề bù)
Suy ra: ∠ A 1 + ∠ A 2 + ∠ B 1 + ∠ B 2 + ∠ C 1 + ∠ C 2 + ∠ D 1 + ∠ D 2 = 180 0 . 4 = 720 0
⇒ ∠ A 2 + ∠ B 2 + ∠ C 2 + ∠ D 2 = 720 0 - ∠ A 1 + ∠ B 1 + ∠ C 1 + ∠ D 1
= 720 0 - 360 0 = 360 0