Hãy liệt kê các phần tử của tập hợp: A = { x ∈ R | x2 + x + 1 = 0}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
1
22 tháng 9 2021
a: \(A=\left\{0;1;2;3;4;5\right\}\)
b: \(B=\left\{2;3;4;5\right\}\)
c: \(C=\left\{0;1;-1;2;-2;3;-3\right\}\)
22 tháng 8 2019
a) Ta có: (2x2 - 5x + 3)(x2 - 4x + 3) = 0
=> \(\orbr{\begin{cases}2x^2-5x+3=0\\x^2-4x+3=0\end{cases}}\)
=> \(\orbr{\begin{cases}2x^2-2x-3x+3=0\\x^2-3x-x+3=0\end{cases}}\)
=> \(\orbr{\begin{cases}2x\left(x-1\right)-3\left(x-1\right)=0\\x\left(x-3\right)-\left(x-3\right)=0\end{cases}}\)
=> \(\orbr{\begin{cases}\left(2x-3\right)\left(x-1\right)=0\\\left(x-1\right)\left(x-3\right)=0\end{cases}}\)
=> x = 3/2 hoặc x = 1
hoặc : x = 1 hoặc x = 3
=> Tập hợp A = {1; 3/2; 3}
b) Ta có: (x2 - 10x + 21)(x3 - x) = 0
=> (x2 - 7x - 3x + 21)x(x2 - 1) = 0
=> [x(x - 7) - 3(x - 7)x(x2 - 1) = 0
=> (x - 3)(x - 7)x(x - 1)(x+ 1) = 0
=> x - 3 = 0 hoặc x - 7 = 0 hoặc x = 0 hoặc x - 1 = 0 hoặc x + 1 = 0
=> x = 3 hoặc x = 7 hoặc x = 0 hoặc x = 1 hoặc x = -1
=> Tập hợp B = {-1; 0; 1; 3; 7}
17 tháng 8 2022
mày điên à đây là mini world à đây không phải toán lớp 1 con ngu
18 tháng 10 2023
`#3107.101107`
a,
\(\text{A = }\left\{x\in R\text{ | }\left(2x-x^2\right)\left(3x-2\right)=0\right\}\)
`<=> (2x - x^2)(3x - 2) = 0`
`<=>`\(\left[{}\begin{matrix}2x-x^2=0\\3x-2=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x\left(2-x\right)=0\\3x=2\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\2-x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\x=2\\x=\dfrac{2}{3}\end{matrix}\right.\)
Vậy, `A = {0; 2; 2/3}`
b,
\(\text{B = }\left\{x\in R\text{ | }2x^3-3x^2-5x=0\right\}\)
`<=> 2x^3 - 3x^2 - 5x = 0`
`<=> x(2x^2 - 3x - 5) = 0`
`<=>`\(\left[{}\begin{matrix}x=0\\2x^2-3x-5=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\2x^2-2x+5x-5=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\\left(2x^2-2x\right)+\left(5x-5\right)=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\2x\left(x-1\right)+5\left(x-1\right)=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\\left(2x+5\right)\left(x-1\right)=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\2x+5=0\\x-1=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\\x=1\end{matrix}\right.\)
Vậy, `B = {-5/2; 0; 1}.`
18 tháng 10 2023
c,
\(\text{C = }\left\{x\in Z\text{ | }2x^2-75x-77=0\right\}\)
`<=> 2x^2 - 75x - 77 = 0`
`<=> 2x^2 - 2x + 77x - 77 = 0`
`<=> (2x^2 - 2x) + (77x - 77) = 0`
`<=> 2x(x - 1) + 77(x - 1) = 0`
`<=> (2x + 77)(x - 1) = 0`
`<=>`\(\left[{}\begin{matrix}2x+77=0\\x-1=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}2x=-77\\x=1\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=-\dfrac{77}{2}\\x=1\end{matrix}\right.\)
Vậy, `C = {-77/2; 1}`
d,
\(\text{D = }\left\{x\in R\text{ | }\left(x^2-x-2\right)\left(x^2-9\right)=0\right\}\)
`<=> (x^2 - x - 2)(x^2 - 9) = 0`
`<=>`\(\left[{}\begin{matrix}x^2-x-2=0\\x^2-9=0\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x^2+x-2x-2=0\\x^2=9\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}\left(x^2+x\right)-\left(2x+2\right)=0\\x^2=\left(\pm3\right)^2\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x\left(x+1\right)-2\left(x+1\right)=0\\x=\pm3\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}\left(x-2\right)\left(x+1\right)=0\\x=\pm3\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x-2=0\\x+1=0\\x=\pm3\end{matrix}\right.\)
`<=>`\(\left[{}\begin{matrix}x=2\\x=-1\\x=\pm3\end{matrix}\right.\)
Vậy, `D = {-1; -3; 2; 3}.`
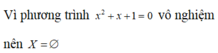
Do phương trình x2 + x + 1 = 0 vô nghiệm nên tập hợp A không có phần tử nào