Giả sử x = a / m, y = b / m (a, b, m ∈ Z, m > 0) và x < y. Hãy chứng tỏ rằng nếu chọn Z = 2 a + 1 2 m thì ta có x < z < y.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 6 2017
theo đề bài ta có :
\(x=\frac{a}{m}\); \(y=\frac{b}{m}\)( a,b,m \(\in\)Z , m > 0 )
vì x < y \(\Leftrightarrow\)\(\frac{a}{m}< \frac{b}{m}\)
\(\Rightarrow a< b\Rightarrow a+a< b+a\Rightarrow2a< a+b\)
\(\Rightarrow\frac{2a}{2m}< \frac{a+b}{2m}\Rightarrow\frac{a}{m}< \frac{a+b}{2m}\Rightarrow x< z\left(1\right)\)
Vì a < b \(\Rightarrow\)a + b < b + c
\(\Rightarrow a+b< 2b\)
\(\Rightarrow\frac{a+b}{2m}< \frac{2b}{2m}\Rightarrow\frac{a+b}{2m}< \frac{b}{m}\Rightarrow z< y\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)\(x< z< y\)
S
12 tháng 6 2017
Theo bài ra ta có \(x< y\Rightarrow\frac{a}{m}< \frac{b}{m}\Rightarrow\frac{a}{2m}< \frac{b}{2m}\)
\(\Rightarrow\frac{a}{2m}+\frac{a}{2m}< \frac{a}{2m}+\frac{b}{2m}\Rightarrow\frac{2a}{2m}< \frac{a+b}{2m}\Rightarrow\frac{a}{m}< \frac{a+b}{2m}\Rightarrow x< z\) (1)
Từ x < y, ta lại có \(\frac{a}{2m}< \frac{b}{2m}\Rightarrow\frac{a}{2m}+\frac{b}{2m}< \frac{b}{2m}+\frac{b}{2m}\Rightarrow\frac{a+b}{2m}< \frac{2b}{2m}\Rightarrow\frac{a+b}{2m}< \frac{b}{m}\Rightarrow z< y\) (2)
Từ (1) và (2) suy ra đpcm
17 tháng 8 2016
Ta có x=\(\frac{a}{m}=\frac{2a}{2m}\) , y=\(\frac{b}{m}=\frac{2b}{2m}\)
Vì x<y nên a<b
Có a<b =>2a<a+b (1)
Có a<b =>a+b<2b (2)
Từ (1) và (2) =>2a<a+b<2b =>\(\frac{2a}{2m}< \frac{a+b}{2m}< \frac{2b}{2m}\)
=>x<y<z ( đpcm)
20 tháng 8 2018
ta có: x<y hay \(\frac{a}{n}< \frac{b}{m}\Rightarrow a< b\)
so sánh x,y,z ta chuyển chúng cùng mẫu: 2m
\(x=\frac{a}{m}=\frac{2a}{2m}\) và \(y=\frac{b}{m}=\frac{2b}{2m}\) và \(z=\frac{\left(a+b\right)}{2m}\)
mà a<b
suy ra: a+a<b hay 2a<a+b
=> x<z (1)
mà a<b
suy ra: a+b<b+b hay a+b<2b
=> z<y (2)
từ (1) và (2) => x<z<y
vậy x<z<y
hpk tốt
17 tháng 6 2015
Ta có:x=\(\frac{a}{m}\)<=>x=\(\frac{2a}{2m}\)
y=\(\frac{b}{m}=>y=\frac{2b}{2m}\)
z=\(\frac{\left(a+b\right)}{2m}\)
mà x<y nên a<b (với m>0)
=>a+a<a+b<b+b
hay 2a<a+b<2b
=>\(\frac{2a}{2m}
NT
giả sử x=a/m, y=b/m(a,b ,m thuộc z, m>0)và x<y. Hãy chứng tỏ rằng nếu chọn z=a+b/2m thì ta có x<z<y.
3
19 tháng 8 2016
Ta có
\(x=\frac{a}{m}=\frac{2a}{2m}\) ; \(y=\frac{b}{m}=\frac{2b}{2m}\)
Vì a<b nên 2a<a+b (1)
Vì a<b nên a+b<2b (2)
Từ (1) và (2) =>2a<a+b<2b
=>\(\frac{2a}{2m}< \frac{a+b}{2m}< \frac{2b}{2m}\)
=>x<z<y ( đpcm)
CG
24 tháng 8 2018
cm x < z: z = (a + b)/2m > (a + a)/2m = 2a/2m = a/ m = x => z >x
cm : z < y: z = (a + b)/2m < (b + b)/2m = 2b/2m = b/m = y
24 tháng 8 2018
Ta có : x=a/m : y=b/m (m>0)
Vì x<y =>a<b
x=a/m=2a/2m=a+a/2m<a+b/2m(a<b)(1)
y=b/m=2b/2m=b+b/2m>a+b/2m(b>a)(2)
Từ (1)(2)=>a+a/2m<a+b/2m + b+b/2m
=>x<z<y
Vì x < y nên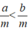
mà m > 0 nên a < b. Ta có
Chọn số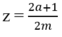
. Do 2a < 2a + 1 và m > 0 nên 
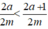hay x < z. (1)
Do a < b và a; b ∈ Z nên a + 1 ≤ b suy ra 2a + 2 ≤ 2b.
Ta có 2a + 1 < 2a + 2 ≤ 2b nên 2a + 1 < 2b, do đó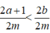
hay z < y. (2)
Từ (1) và (2) suy ra: x < z < y