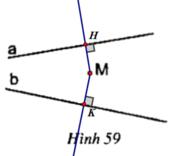
Cho điểm M và hai đường thẳng a, b không song song với nhau (h.59)
Nêu tên các cặp góc bằng nhau, bù nhau.
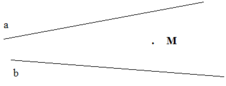
Hình 59
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
4 tháng 9 2018
Lời giải chi tiết
a) Trước hết, ta nêu cách vẽ một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
1. Cách vẽ dùng ê ke và thước kẻ:
+ Cho trước đường thẳng p và M ∉ p.
Đặt một lề ê ke trùng với p, dịch chuyển ê ke trên p sao cho lề thứ hai của ê ke sát vào M
+ Cho trước đường thẳng p và M∈pM∈p
Đặt một lề ê ke trùng với p và dịch chuyển ê ke trên p sao cho góc ê ke trùng với M.
2. Cách vẽ dùng compa và thước kẻ:
+ Cho trước đường thẳng p và M ∉ p.
Vẽ đường thẳng qua M vuông góc với p.
Chọn trên p hai điểm A và B.
Vẽ các đường tròn (A; AM) và (B; BM)
Hai đường tròn này cắt nhau tại M và M’ thì NM’ vuông góc với p
Chú ý: Có thể xem bài tập 51 phần hình học. Cho trước đường thẳng p và
Vẽ đường thẳng vuông góc với p tại M
Dùng compa vẽ đường tròn (M; r1) cắt p tại A và B. Vẽ các đường tròn (A;r2) và (B; r2) với r2 > r1.
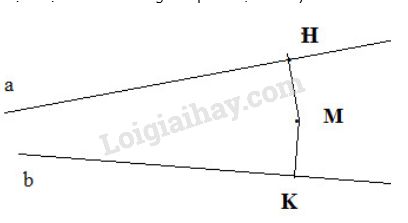
Các đường tròn này cắt nhau tại E và F thì đường thẳng EF vuông góc p tại M. Bây giờ ta theo một trong hai cách vẽ nêu trên vẽ đường thẳng qua M vuông góc a tại H và đường thẳng qua M vuông góc với b tại K
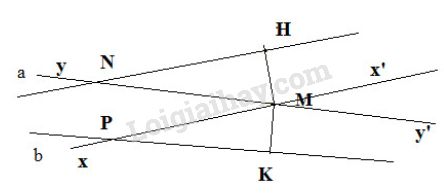
b) Vẽ đường thẳng xx’ vuông góc với MH tại M và đường thẳng yy’ vuông góc với MK tại M thì xx’ // a (vì cùng vuông góc với MH) và yy’ //b.
c) Giả sử a cắt yy’ tại N và b cắt xx’ tại P.
Một số cặp góc bằng nhau là góc x'My' và x'Pk , HNM và MPK
Một số cặp góc bù nhau, chẳng hạn như góc HNM và nMx' , kPm và pMy'
H
19 tháng 4 2017
a) Trước hết, ta nêu cách vẽ một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
1.Cách vẽ dùng ê ke và thước kẻ:
+Cho trước đường thẳng p và M ∉ p.
Đặt một lề ê ke trùng với p, dịch chuyển ê ke trên p sao cho lề thứ hai của ê ke sát vào M
+Cho trước đường thẳng p và M∈pM∈p
Đặt một lề ê ke trùng với p và dịch chuyển ê ke trên p sao cho góc ê ke trùng với M.
2.Cách vẽ dùng compa và thước kẻ:
+Cho trước đường thẳng p và M ∉ p.
Vẽ đường thẳng qua M vuông góc với p.
Chọn trên p hai điểm A và B.
Vẽ các đường tròn (A; AM) và (B; BM)
Hai đường tròn này cắt nhau tại M và M’ thì NM’ vuông góc với p
Chú ý: Có thể xem bài tập 51 phần hình học. Cho trước đường thẳng p và
Vẽ đường thẳng vuông góc với p tại M
Dùng compa vẽ đường tròn (M; r1) cắt p tại A và B. Vẽ các đường tròn (A;r2) và (B; r2) với r2 > r1.
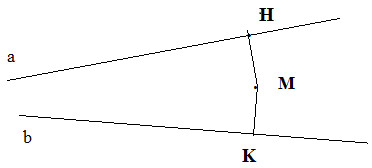
Các đường tròn này cắt nhau tại E và F thì đường thẳng EF vuông góc p tại M. Bây giờ ta theo một trong hai cách vẽ nêu trên vẽ đường thẳng qua M vuông góc a tại H và đường thẳng qua M vuông góc với b tại K
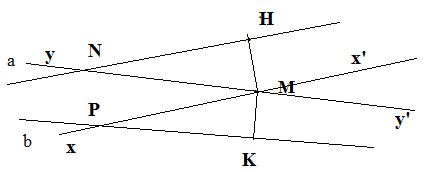
b) Vẽ đường thẳng xx’ vuông góc với MH tại M và đường thẳng yy’ vuông góc với MK tại M thì xx’ // a (vì cùng vuông góc với MH) và yy’ //b.
c) Giả sử a cắt yy’ tại N và b cắt xx’ tại P. Một số cặp góc bằng nhau là x’My’ và x’PK, HNM và MPK.
Một số cặp góc bù nhau, chẳng hạn như HNM và NMx’, KPM và PMy’.
11 tháng 7 2017
Lời giải
a) Sử dụng êke
- Đặt một cạnh góc vuông đi qua điểm M, dịch chuyển cạnh còn lại trùng với đường thẳng a. Ta vẽ được đường thẳng MH ⊥ a.
- Làm tương tự ta vẽ được đường thẳng MK ⊥ b.
b) Sử dụng êke
- Đặt êke sao cho điểm góc vuông đi qua điểm M, dịch chuyển êke để một cạnh vuông trùng với MH, ta vẽ được đường thẳng xx' ⊥ MH. Từ đó suy ra xx' // a (vì cùng ⊥ MH).
- Làm tương tự ta vẽ được đường thẳng yy' // b.
c) Giả sử a cắt yy' tại N và b cắt xx' tại P.
CM
7 tháng 5 2017
Sử dụng êke
Trước hết, ta nêu cách vẽ một đường thẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước
Cách vẽ dùng êke và thước kẻ:
- Cho trước đường thẳng a và M ∉ a.
Đặt một lề êke trùng với a, dịch chuyển êke trên a sao cho lề thứ hai của êke sát vào M
- Vẽ đường thẳng sát lề thứ hai của êke qua M cắt a tại H, ta được MH ⏊ a tại H ∈ a
Tương tự vẽ MK ⏊ b tại K ∈ b.
CM
6 tháng 1 2019
Sử dụng êke
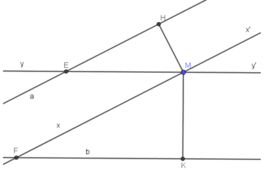
* Để vẽ đường thẳng xx’ đi qua M và song song với a, ta chỉ cần vẽ đường thẳng vuông góc với MH.
Thật vậy vì xx’ ⏊ MH, MH ⏊ a ⇒ xx’ // a.
Cách vẽ:
Đặt ê ke sao cho đỉnh góc vuông trùng với điểm M, một cạnh góc vuông trùng với MH.
Vẽ đoạn thẳng trùng với cạnh góc vuông còn lại của eke.
Kéo dài đoạn thẳng ta được đường thẳng xx’ cần vẽ.
* Tương tự với đường thẳng yy’
CM
1 tháng 8 2019
Dùng ê ke để vẽ, ta được tứ giác ADBC như sau:
Trong tứ giác ADBC có:
- Cặp cạnh AD và BC song song với nhau
- Cặp cạnh AB và DC song song với nhau.
CM
23 tháng 7 2018
Dùng ê ke để vẽ, ta được tứ giác ADBC như sau:
Trong tứ giác ADBC có:
- Cặp cạnh AD và BC song song với nhau
- Cặp cạnh AB và DC song song với nhau.
CM
9 tháng 11 2019
Nếu một đường thẳng cắt hai đường thẳng song song thì theo tính chất của hai đường thẳng song song ta có:
+) Mỗi cặp góc so le trong bằng nhau.
+) Mỗi cặp góc đồng vị bằng nhau.
+) Mỗi cặp góc trong cùng phía bù nhau.
Do đó, các kết quả trên đều đúng
Giả sử a cắt yy’ tại E và b cắt xx’ tại F.
- Một số cặp góc bằng nhau: